Available Languages
- Consultez cette page en FRANÇAIS
- Consult this page in ENGLISH
Structure, Semiotic Relations and Homologation1
1. ABSTRACT
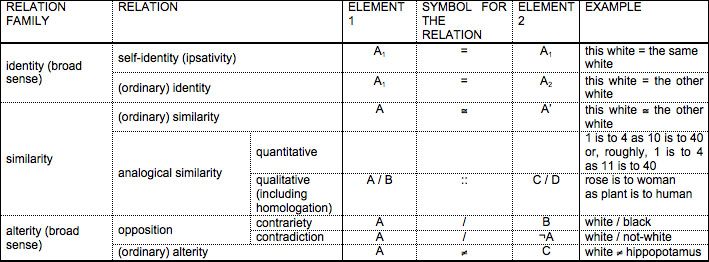
A structure is composed of at least two elements, known as terms, with at least one relation established between them. By formulating a typology of relations, we can predict various kinds of structures. Distinctions can be drawn between comparative relations (identity, similarity, alterity, opposition, homologation, etc.), presential relations (presupposition, mutual exclusion, etc.), and others. From among the many simple structures used to characterize the role of signifiers (elements of expression) and/or signifieds (content) in a semiotic act, we have chosen to focus on homologation. Homologation is the relation between (at least) two pairs of opposite elements, such that for two oppositions A/B and C/D, one can say that A is to B as C is to D. For example, in a particular text, life (A) is to death (B) as positive (C) is to negative (D).
This text is a new version of the text in this book:
Louis Hébert, Dispositifs pour l'analyse des textes et des images, Limoges, Presses de l'Université de Limoges, 2007.
Click here to obtain the English translation of this book. (pdf)
This text may be reproduced for non-commercial purposes, provided the complete reference is given:
Louis Hébert (2011), “Structure, Semiotic Relations and Homologation”, in Louis Hébert (dir.), Signo [online], Rimouski (Quebec), http://www.signosemio.com/structure-semiotic-relations-homologation.asp.
An updated and extended version of this chapter can be found in Louis Hébert, An Introduction to Applied Semiotics: Tools for Text and Image Analysis (Routledge, 2019, www.routledge.com/9780367351120).
2. THEORY
2.1 STRUCTURE DEFINED
We will posit that any signifying unit -- except for signifying units that are considered impossible to break down, not from a purely methodological standpoint, but de facto -- may be analyzed in terms of structure, and that any structure is an entity that may be broken down into at least two terms (or relata -- relatum in the singular) linked by at least one relation (or function). Generally speaking, the inventory of terms is in opposition with the inventory of relations, in that the terms are a priori undefined in number, and the relations are a priori limited in number (although the inventory of relations can be partially open and can vary according to the analytical objectives and the type of objects being analyzed).
We will say that the minimal structure is composed of two terms linked by only one relation (one relation that we are describing, anyway). Thus, fire/water is a minimal structure (of the signified) in "firewater", whose terms are related by opposition. In "fire is luminous water", the oppositional relation is accompanied by a comparative relation (a metaphor).
NOTE: OTHER POSSIBLE DEFINITIONS OF THE MINIMAL STRUCTURE
Our definition of the minimal structure can be expanded to include cases in which the relation is established between a term and itself (a reflexive relation). Hjelmslev gives a more restrictive definition of the minimal structure than ours; he views a structure as "an autonomous entity of internal dependencies", i.e., a relation between relations. By this definition, the minimal structure would entail two relations linked by a third relation, and would customarily include four elements. A homology between two oppositions is in fact a minimal structure of this kind. However, other kinds of minimal structures are possible. Suppose that r = a relation and R = a relation between relations. A minimal structure might include only two elements. They will be linked either by two different relations: (A r1 B) R (A r2 B) or (A r1 A) R (A r2 B); or by a single relation:(A r1 B) R (A r1 B) or (A r1 A) R (A r1 B). Lastly, a structure could even theoretically comprise just one term, linked to itself, but probably only if the two relations are different: (A r1 A) R (A r2 A).
2.2 STRUCTURES COMPOSED OF SIGNIFIERS, SIGNIFIEDS AND SIGNS
With respect to the signifier/signified opposition (or expression/content) constituting any sign, there are three basic kinds of structural analysis one can perform, depending on whether the structure includes (1) only the signifier (e.g., an analysis restricted to the versification of a poem), (2) only the signified (e.g., a traditional thematic analysis), or (3) both the signifier and the signified (e.g., an analysis of the relations between the sounds and the meanings of the words used for rhyming in a poem).
2.3 A TYPOLOGY OF RELATIONS
By formulating a typology of relations, we can predict various kinds of structures. A relation may be characterized according to numerous criteria. We will distinguish somewhat arbitrarily between what we will call formal criteria (reflexive/transitive, directional/non-directional, monadic/polyadic relations, and others) and what we will call semantic criteria (comparative relations, such as identity, similarity, alterity, opposition, homologation; presential relations, such as presupposition and mutual exclusion; and others).
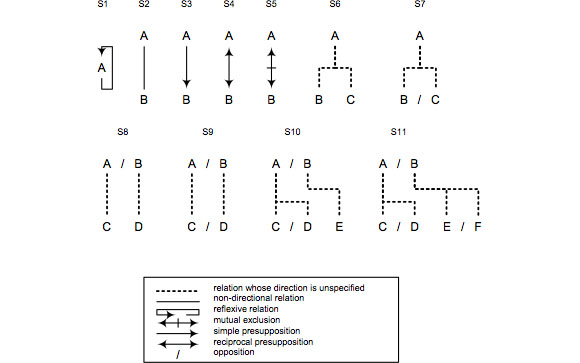
The following diagram illustrates a few possible structures. They were produced by combining some formal criteria (such as direction and the number of elements linked together) and some semantic criteria (opposition and presupposition, among others) by which we can characterize the relations.
In order to increase the representational capabilities of our diagram, for the structures that include three terms or more (from S6 to S11), we have chosen to leave the directional status of the relations undetermined (as indicated by the dotted lines). We can give a profusion of specifications for these undetermined relations, such as non-directional, unidirectional, and so forth. We can have a structure S6a, for example, in which B and C are linked to A by a relation of simple presupposition (unidirectional, therefore). Likewise, we can derive numerous other structures from the ones given here by adding terms or by adding semantic relations. For instance, if we add a relation of opposition between D and E in structure 10, we obtain a new structure, in which an opposition between two terms is linked to an opposition between three terms2.
Diagram of some possible structures
2.3.1 FORMAL TYPOLOGIES
2.3.1 MONADIC / POLYADIC RELATIONS
Depending on the number of terms linked together, we refer to a relation as monadic (S1) or polyadic (S2, S3, S4 and S5 are dyadic; S6 and S7 are triadic; S8 and S9 are tetradic, S10 is pentadic, and so on).
2.3.1.2 REFLEXIVE / TRANSITIVE RELATIONS
A relation is said to be reflexive if it links a term to itself (S1). It is said to be transitive if it links a term to one (S2, for example) or more other terms.
To take a grammatical example, in "She dressed herself", "dressed" is a reflexive verb, in that the action of dressing starts and ends with "she", so to speak; conversely, in "She dressed her daughter", "dressed" is a direct transitive verb, since the action starts with "she" and crosses over to "her daughter", ending there. Another example is the poetic function -- one of the functions of language as defined by Jakobson --, which consists of a reflexive relation in which the message refers to itself. All relations whose names use the prefixes "self-" and "auto-" are reflexive (self-definition, self-representation, autoreference, etc.). We will come back to this later.
NOTE: REFLEXIVE / TRANSITIVE RELATIONS AND MONADIC / POLYADIC RELATIONS
A monadic relation is necessarily reflexive (a single element is linked to itself); a polyadic relation is necessarily transitive (at the same time, it can be partly reflexive).
2.3.1.3 NON-DIRECTIONAL / DIRECTIONAL RELATIONS
A relation is said to be non-directional when it is established either by the facts or through methodological reduction (by intentional simplification, made explicit and justified) that it is not directed toward one of the terms involved (S2, for example)3. A relation is said to be directional when it is said to go from one or more source terms to one or more target terms. It is said to be unidirectional, or asymmetrical, or non-reciprocal, if it goes from one or more source terms to one or more target terms, but not the reverse (S3, for instance); if the reverse is also true, then it is a bidirectional, or symmetrical, or reciprocal relation (S4 and S5, for instance).
2.3.2 SEMANTIC TYPOLOGIES
We propose a methodological distinction between four basic kinds of semantic relations: (1) comparative relations: identity, similarity, alterity, opposition, homologation, etc.; (2) temporal relations: simultaneity and succession, etc.; (3) presential relations: simple presupposition, reciprocal presupposition and mutual exclusion; (4) relations of inclusion: set relations (involving classes and/or elements thereof), mereological relations (involving wholes and/or parts), and type-token relations (involving types and/or tokens); and (5) other semantic relations.
2.3.2.1 TEMPORAL AND SPATIAL RELATIONS
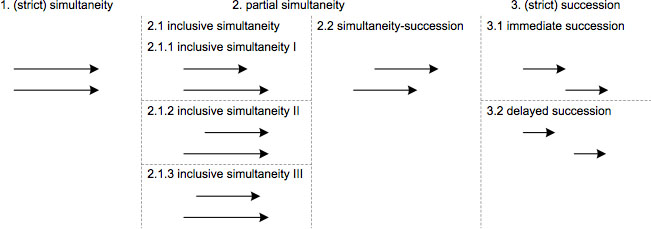
Simultaneity (or concomitance) is the relation between terms associated with the same initial and final temporal positions, and thus with the same temporal extent (duration). We can distinguish between strict simultaneity (1) (as in our definition) and the following kinds of partial simultaneity (2): inclusive simultaneity (2.1) (in which the first time period is entirely contained within the second, and is exceeded by it); inclusive simultaneity in which the initial positions coincide (2.1.1); inclusive simultaneity in which the final positions coincide (2.1.2); inclusive simultaneity in which the initial and final positions do not coincide (2.1.3); simultaneity-succession (2.2) (partial simultaneity and succession).
Succession (3) is the relation between terms in which the final temporal position of one term precedes the initial position of the other term. Immediate succession (3.1) implies that the initial position of the second term comes immediately after the final position of the first term; otherwise we have mediate or delayed succession (3.2). A distinction can be made between strict succession (3) (addressed in the preceding definitions) and simultaneity-succession (2.2), a form of partial simultaneity and succession.
The following diagram illustrates the main dyadic temporal relations.
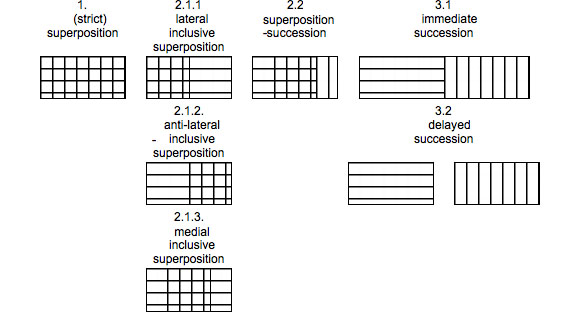
These temporal relations have spatial correspondents, and thus, through generalization, they are relations of extent, whether the extent is spatial or temporal; but other spatial relations exist as well. The spatial relations that coincide with temporal relations are illustrated in the following diagram by combining a horizontally striped box with a vertically striped box in various ways. To simplify, we have used "transparent" shapes that allow us to see what is behind them; the same relations can use opaque shapes. To further simplify, only the width of the boxes was varied. For example, horizontal and vertical medial superposition implies an inclusion in both width and height, not just width, as shown here. With three-dimensional shapes, one must also take depth into consideration. Clearly, spatial relations are not restricted to those shown in the diagram or those we have just proposed in order to expand the diagram and the typology.
Dyadic spatial relations
2.3.2.2 PRESENTIAL RELATIONS
A presential relation is a relation in which the presence or absence of one term indicates the presence or absence of another term.
Presupposition is a relation in which the presence of one term (the presupposing term) indicates the presence of another term (the presupposed term). This type of relation can be described as "both ... and ..." (both one term and the other term). Simple presupposition (or unilateral dependence) is a unidirectional relation (A presupposes B, but not the reverse). For example, the presence of a wolf presupposes the presence of a mammal (since the wolf is a mammal), but the presence of a mammal does not presuppose the presence of a wolf (since the mammal could be a dog, for instance). Reciprocal presupposition (or interdependence) is a bidirectional relation (A presupposes B and B presupposes A. For example, the back side of a sheet of paper presupposes the front, and vice versa; in fact, there is no front without a back, and vice versa. We can represent simple presupposition by an arrow (A presupposes B would be written as: A → B, or B ← A) and reciprocal presupposition by an arrow with two heads (A ↔ B).
Mutual exclusion is the relation between two elements that cannot be present together. This type of relation can be described as "either ... or ..." (either one term or the other term). For example, in reality, a single element cannot be alive and dead at the same time (which does not necessarily apply in a semiotic act, such as a fantasy story)4. We can represent mutual exclusion by using two arrows pointing toward each other (A →← B) or a vertical line (A | B).
If the presence of the terms is viewed not from a categorial standpoint (of all or nothing), but from a gradual (and thus quantitative) standpoint, two types of correlation may then be found between two terms. The correlation is said to be direct if (1) an increase in A leads to an increase in B and vice versa, and (2) a decrease in A leads to a decrease in B and vice versa. A direct correlation, thus, is a "more... more..." or "less... less..." type of correlation. For example, when the kinetic energy of a car increases, its speed also increases, and if its speed increases, its kinetic energy does, too.
The correlation is said to be inverse if (1) an increase in A leads to a decrease in B, and an increase in B leads to a decrease in A, and (2) a decrease in A leads to an increase in B and a decrease in B leads to an increase in A. An inverse correlation, thus, is a "more... less..." or "less... more..." type of correlation. For a constant quantity of gas at a constant temperature, pressure and volume are inversely correlated; i.e., if the volume is increased, the pressure decreases, and if the pressure increases, it is because the volume has decreased.
Direct and inverse correlation can be compared to reciprocal presupposition and mutual exclusion, respectively. That is, in a direct correlation, by raising the degree of presence of one term, I increase the presence of another5 ; in an inverse correlation, by raising the degree of presence of one term, I decrease the presence of another (or in other words, I increase its degree of absence). For more details, see the chapter on the tensive model.
A presential relation is not necessarily coupled with any relation, i.e., joining a cause to an effect, or a non-effect to a cause or the absence of a cause. The following is a presential relation not coupled with a causal relation: A few decades ago (perhaps it's still true), if you changed your altitude, you also changed your chances of dying of a lung disease; to be precise, the two variables were directly related. It would be wrong to think that altitude was harmful to the lungs; it was just that those who were seriously ill were advised to live in the mountains. The following is a presential relation coupled with a causal relation: An explosion is necessarily caused by an explosive substance, and it presupposes an explosive substance (but the explosive substance does not necessarily involve an explosion).
A presential relation is not necessarily coupled with any particular temporal relation: all presential relations can be combined with succession or simultaneity. For example, "wolf" presupposes "mammal", since a wolf is necessarily a mammal (but not the reverse: a mammal is not necessarily a wolf); Therefore we can say that "wolf" and "mammal" are simultaneously present. (We can also take the view that there is a lack of temporal relation: a sort of atemporal logical present.) However, a bank robbery necessarily presupposes a previous stage, even reduced to the simplest terms, such as coming up with a plan (but the reverse does not hold: coming up with a plan does not necessarily imply that it will be carried out). This illustrates our view that presupposition is not correlated a priori with a temporal relation, despite the presence of the prefix "pre-"; however, in order to avoid violent semantic shocks, we can use the term "implication" when the presupposed element is temporally posterior (this is why we have said that coming up with a plan does not necessarily imply carrying it out). For examples of combinations of presential and temporal relations, see the chapter on the narrative program.
2.3.2.3 COMPARATIVE RELATIONS
Strictly speaking, identity is the relation between terms that have all identical characteristics. Alterity is the relation between terms that possess no identical characteristics. As we can see, this brings in the distinction between the whole (that which has characteristics) and the parts (the characteristics). Absolute identity does not exist for material objects: two "identical" sheets of paper will prove to be non-identical under a microscope. It is questionable whether it exists even for mental objects: two "identical" triangles with exactly the same spatial coordinates must be distinguishable (even just by "labeling" them "triangle A" and "triangle B"), which presumes some form of non-identity. In fact, identity in the strict meaning is certain only for ipsativity, an element's identity with itself (provided we subscribe to the thesis that a self-identity exists).
NOTE: COMPARABILITY
Given the possibility of strict identity and alterity, "comparability" is the name we will give to a relation of partial identity/alterity. Similarity is the term we will use for the sub-species of comparability in which identity prevails over alterity (but in which at least one unshared characteristic remains); it can be represented by the approximate equality sign (@). Mathematically speaking, in minimum similarity we find 50% + 1 identities; in maximum similarity, we find 100% - 1 identities. Dissimilarity is the term we will use for the other sub-species of comparability, in which alterity prevails over identity (but in which at least one common characteristic remains); it can be represented by the unequal sign (¹). Mathematically speaking, in minimum dissimilarity we find 50% + 1 alterities; in maximum dissimilarity, we find 100% - 1 alterities. Assimilarity is the term we will use for the sub-species of comparability in which identity and alterity are equal, i.e., 50% identities and 50% alterities, mathematically.
Of course, through methodological reduction (i.e., intentional, made explicit and relevant), we can have identity in the broad sense and alterity in the broad sense. This reduction may be functional, in particular: it matters little which piece of blank paper I write on -- they are "identical". In the broad sense, identity is then the relation between terms whose strength and/or number of identical characteristics predominate over the strength and/or number of non-identical characteristics. In the broad sense, alterity is the relation between terms whose strength and/or number of non-identical characteristics predominate over the strength and/or number of identical characteristics.
The relation of similarity can be placed in the vicinity of identity, as it is an attenuated form of identity. There is a distinction to be made between ordinary similarity and analogical similarity. The latter takes two forms: quantitative analogical similarity (as in mathematical proportions -- 1 is to 4 as 10 is to 40) and qualitative analogical similarity (as in metaphors and homologies, either metaphorical or not -- a woman is to a rose as the human order is to the plant order). We will treat homologation as a complex form of comparative relation. As we will see later, it involves relations of opposition, similarity, presupposition and mutual exclusion; however, on the whole, it can be regarded as a relation of similarity, or more accurately, of qualitative analogical similarity.
In theory, on the scale of alterity/identity, there is a zone where the alterities and identities between characteristics are equal in strength and/or number. In practice, no doubt, this neutral zone, defined by a relation that can be termed identity-alterity, emerges only rarely, since the adjacent zones of identity and alterity draw in the values likely to fit there by "rounding" them.
There is a distinction to be made between ordinary identity -- or just identity -- and ipsative identity, which is an element's self-identity (an element is identical to itself). Transformation is the process or operation whose outcome is to establish a comparative relation other than identity between what a term was and what it has become. The word also designates the result of this process. Transformation may be represented by an apostrophe, where O' indicates the transformation of an object O, for instance.
Opposition is a relation between terms that are more or less incompatible. We can distinguish two kinds of opposition: contrariety (e.g., true / false, life / death, rich / poor) and contradiction (e.g., true / not-true, life / not-life, rich / not-rich). For example, a contradiction occurs in The Treachery of Images by Magritte, a painting representing a pipe (pipe term) with the caption [translated]: "This is not a pipe." (non-pipe term). As we can see, the contradiction can be made between one semiotics and another. It can even occur within a non-linguistic semiotics, e.g., if a painting represents the same individual alive and dead. The Aristotelian contradiction presumes (1) the presence of a relation of contradiction (2) within the same object (3) seen from the same point of view. That is, supposing that empty and full form a contradiction, a piece of Swiss cheese (or a doughnut) is the scene of a relation of contradiction, but not an Aristotelian contradiction, since empty and full don't apply to the same parts of the cheese. Aristotelian contradictions often dissolve completely or partially through dissimilation, a differentiation of relationships. For example, "Your son [paternity] is not your son [property]" (Confucius), and "Black [emotional darkness] sun [physical brightness] of melancholy" (Nerval). Contrariety is a relation of opposition in which incompatibility is minimal, and contradiction is a relation of opposition in which incompatibility is maximal. Mutual exclusion can be seen as the most fundamental result of a relation of incompatibility, but it seems that not every case of mutual exclusion is built on an opposition (e.g., every time a character is chewing a carrot, he is not chewing a potato, and vice versa). Compatibility can take form as complementarity; but not every compatibility is a case of complementarity: e.g., two identical propositions (like "the earth is round") are compatible, but not complementary. Presupposition can be seen as the most fundamental result of a relation of complementarity (notably as a relation that, in a semiotic square, becomes established between not-true and false, to give an example).
In practice, how do we distinguish contrariety from contradiction, since not every contradiction is necessarily expressed with the privative "not-"? We will say that contradiction is categorial and that contrariety is gradual. For example, in classical logic, true and false are contradictories, since not-true equals false and not-false equals true; however, rich and poor are contraries, since not-rich does not necessarily equal poor, and not-poor does not necessarily equal rich.
Opposition can be viewed in several different ways: as a comparative relation at the same level as alterity and identity, or as a subspecies of alterity, or as a subspecies of similarity, among others. Actually, elements set in opposition are comparable, and therefore similar: for example, day and night are opposable because both are time spans in a day (a shared property). A forward slash represents a relationship of opposition between terms, such as life / death. The production of a contradictory term may be indicated by the logical negation symbol (e.g., ¬life means not-life).
In semiotics, when both terms of an opposition are co-present in a single semiotic act, it is termed a contrast. For example, for the opposition water/fire in "They get along like water and fire", we have contrast. We have non-contrast when one of the terms of the opposition remains virtual by not appearing in the semiotic act, e.g., "fire" in "I'm drinking water". Obviously, it is possible that none of the terms of the opposition will appear in the semiotic act, e.g., "I'm eating an apple". The contrast will vary in force depending on how close together the two terms are in the distribution of signs (if "life" is the first word of a linguistic sequence and "death" the second, the contrast will be forceful) and/or whether they relate ("this death-life") or do not relate to the same object ("this person is alive and this other one is dead"). For a more in-depth analysis of the notion of opposition, refer to the chapter on the semiotic square.
NOTE: COMPARATIVE RELATIONS AND RELATIONS OF COMPARISON
We must distinguish a comparative relation from the (metaphorical) relation of comparison that can be established within a semiotic act between a comparing term and a compared term. For instance, in Baudelaire's poem "The Albatross", a metaphorical comparison is created between the poet (compared) and an albatross (comparing).
The following table gives the main comparative relations
2.3.2.4 RELATIONS OF INCLUSION
Three kinds of including/included states are distinguished here, along with the three families of relations and three families of operations that they define. Mereological or holistic inclusion involves wholes (such as a word) and parts (such as the letters in the word). Set inclusion involves classes (such as the class of words) and elements (such as a particular word). Typological inclusion involves types (models, such as the sonnet genre) and tokens (more or less complete manifestations of a model or type, such as a particular sonnet that is more or less regular).
NOTE: THE DIFFERENCE BETWEEN A CLASS AND A TYPE
What exactly is the difference between a type (e.g., the poetry genre) and a class (e.g., the class of poems)? Strictly speaking, a type is not a class because rather than containing, or bringing together the token units (the poems) governed by it, it generates them. We will distinguish between a class's extension (or enumeration) and its intension (or comprehension). For example, the extension of the class of positive whole numbers is: 1, 2, 3, 4, and so on. The intension -- the definition of this class -- is the principle that must be followed by the elements of this class, which in this case is to be a positive whole number. The distinction between a type and the definition, or intension, of a class may seem vague, but they are indeed two distinct things. Type and definition are necessarily abstract entities; token and element can be concrete (this poem as a representative of the poetry genre; this marble as a member of the class of the marbles in this bag) as well as abstract (this love, which is a manifestation of love; humiliation, a member of the class of negative emotions). The difference lies elsewhere. The type is an abstract "individual" that is the result of an induction made from what will become its tokens, relative to which it subsequently acquires the status of a generative entity (as opposed to genetic)6. The definition of a class is not an individual entity, but rather an inventory of one or more properties, optionally accompanied by rules for evaluating the membership of the element. This does not keep us from optionally associating a type with a class.The prototype is the token that is considered by a specific observing subject to be the best and/or the most representative of the type (e.g., the apple or the orange for fruits); the other tokens are further removed (e.g., the star fruit and the lychee).
Including/included is a relative status, and including units can be included units elsewhere, and vice versa. That is, a part (e.g., the syllable as part of a word) may be seen as a whole (the syllable as a grouping of phonemes); an element (a mammal in the class of animals) may be seen as a class (a mammal as a class encompassing the class-elements Canidae, Felidae, etc.); and a token (e.g., the drama genre as a token of the generic field of theater) may be seen as a type (historical drama as a sub-genre of the drama generic type).
Of the various operations of including/included relations, there are a few that should be emphasized. Partitioning or decomposition is a (descending) operation that separates out the parts of a whole that was previously unanalyzed (e.g., by stipulating the semes that make up a given signified). Classification is an (ascending) operation by which we index/include an element in a class. The term "classification" also designates the result of classifying: a structure made up of classes and classified elements (e.g., the scientific taxonomies, such as vertebrate / invertebrate animals, etc.). Typing (or categorization) is an (ascending) operation by which a token is subsumed under a type, related to it, and recognized as its emanation or manifestation. These operations are also the basis of the relations. That is, there is a relation of decomposition between the whole and one of its parts, a relation of classification between the element and the class, and a relation of typing between the token and its type.
For each including/included relation, if we distinguish two including units, and two different included units belonging to each of them, we obtain the following relations: (1) between the two including terms; (2) between an including term and its own included term; (3) between an including term and an included term not its own; (4) between two included terms belonging to the same including term; (5) between two included terms, each belonging to a different including term (this relation gives rise to an indirect relation between the two including terms, just as the relation between including terms gives rise to an indirect relation between the terms included therein). Each of these relations can be followed in either direction. For example, the relation between an including term and its included term may go from including to included (a descending relation) and/or from included to including (an ascending relation). To these five dual relations, we can add the reflexive relation (6) between an including term and itself, and (7) between an included term and itself.
We will give an example using type relations established between genres and the texts that may belong to them. The typology is constructed as follows: (1) between one type and another (e.g., between two opposite textual genres); (2) between the type and its own token (e.g., between a genre and the text belonging to it); (3) between a type and a token other than its own (e.g., between a genre and a text belonging to the opposite genre); (4) between one token and another belonging to the same type; (5) between one token and another belonging to another type (e.g., intertextuality between two texts from different genres); (6) between a type and itself; (7) between a token and itself.
NOTE: INTERNAL (INTRA-) RELATIONS
The relations within a whole can be named using the prefix "intra-" (as in intratextuality, a relation between two parts of one text). A type or a class may be viewed from a mereological standpoint. In the case of a type, the parts can be the defining traits of the type (although it is not certain that a type is always equivalent to an inventory of traits, ranked or unranked). With the extension of a class, the parts are obviously the elements; with the intension of a class, i.e., its definition, the parts can be defining traits or parts of the rules for evaluating whether the elements fit within the definition. Relations within a type can be termed "intratype relations", and relations within a class can be termed "intraclass relations". Obviously, the tokens and the elements -- as long as they are considered decomposable -- may have relations between their parts; these can be called intra-token and intra-element relations, respectively.
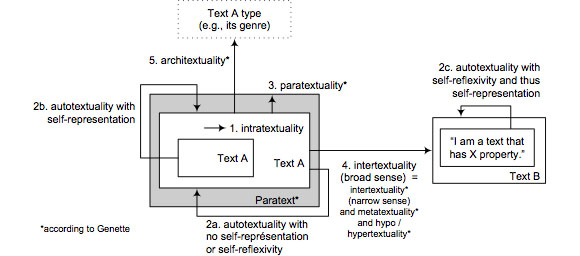
On this basis, we will distinguish several sorts of relations involving text (meant in the broad sense of a semiotic act, such as a text, image, etc.) and generic type ("genre" is meant in the broad sense: genre, discourse, sub-genre, generic form, etc.): autotextuality (relation 7): a text is linked to itself; intertextuality (relation 4 or 5): a text is linked to another text or other texts; architextuality (type 2 or 3 relations): a text token is linked to a text type; autogenericity (a form of autotyping) (relation 6, not shown in the diagram that follows): a type is linked to itself; intergenericity (a form of intertyping) (relation 1, not shown in the diagram that follows): a text type is linked to another text type or other text types. These relations may be viewed as unidirectional, i.e., in one direction or the other (e.g., from the text to its genre or from the genre to the text), or as bidirectional (e.g., from the text to its genre and the reverse).
NOTE: INTERTEXTUALITY ACCORDING TO GENETTE
Genette (1982, p. 8) distinguishes five forms of transtextuality: (a) paratextuality (the relation a text has with its preface, for example); (b) intertextuality (citation, plagiarism, allusion); (c) metatextuality (text commentary by another party); (d) hypertextuality (when a text is grafted onto a prior text, not as commentary, but to transform it (a parody, misrepresentation, transposition), or imitate it (a pastiche, counterfeit, etc.), the former is the hypertext, and the latter is the hypotext); and (e) architextuality (the relation between a text and the classes to which it belongs, such as its genre). Depending on the status assigned to them, Genette's paratextual elements will participate in an intertextual relation (in the expanded sense that we give the term) if one views them as external to the text, or in an intratextual relation if one views them as being internal to the text, or in a strictly paratextual relation. The debate over the intra- or extra-textual nature of the title illustrates the various typological possibilities. For ourselves, we have defined intertextuality in a broader sense than Genette has, one that encompasses what he calls intertextuality, metatextuality, and hyper/hypotextuality; obviously, Genette's distinctions are nonetheless relevant. For details on intertextuality, see Hébert and Guillemette, 2009.
NOTE: TEXTUALITY AND INTRATEXTUALITY
Autotextuality may take several forms: from the text as a whole to itself as a whole, from the whole to a part, from a part to the whole, and lastly, from a part to the same part. When the relation is between a part and another part of the same whole, we have intratextuality. Intertextuality and architextuality may be viewed either as including relations (established between wholes), or as included relations (established first between parts, and indirectly between wholes); in the latter case, the source term is viewed as part of the text, and the target term as part of another text (intertextuality) or part of a text type (architextuality). Moreover, there are included-including relations: e.g., part of a text may evoke the whole of another text or genre (such as the sentence (part) in a novel that says "I've read Hamlet" (whole).
Autotextuality is closely related to the other reflexive relations.
Since autoreference involves a referent -- the third part that we often attribute to the sign, and which we generally define as "the thing we are talking about", the first two parts being the signifier and signified -- it is at once broader than autotextuality (it can involve a sign of any range, and not necessarily a text or complete semiotic act) and also narrower (there is no doubt that not every autotextuality can be considered as an autoreference); if the word "reference" is meant in a broad sense of any referral of one unit to another (which can be itself), then autotextuality is a specific case of autoreference7.
Self-representation (an act represents itself in itself) and self-reflexivity (an act "reflects" on itself in itself) presuppose a relation of autotextuality: that which represents itself or reflects on itself necessarily refers to itself in doing so. Moreover, self-reflexivity presupposes a relation of self-representation: in order to "reflect on itself", the act must somehow present itself as the object of its own discourse. However, not all self-representation is automatically self-reflexive. For example, the Laughing Cow -- the trademark for a well known cheese -- is self-represented in her earrings, but it is difficult to see this as any kind of reflection). Finally, autotextuality -- or self-reference -- may be found by itself, without self-representation or self-reflexivity. For example, the famous political slogan "I like Ike" attracts attention to itself by its sounds, without having any self-reflexivity or actual self-representation.
In summary: all self-reflexivity presupposes self-representation, and all self-representation presupposes autotextuality; however, not all autotextuality is self-representation, and not all self-representation is self-reflexivity. The diagram below illustrates the main textual relations. For the sake of simplicity, we have made the relations unidirectional, but they can also be viewed as unidirectional in the other direction or as bidirectional.
The main textual relations
2.3.2.5 OTHER SEMANTIC RELATIONS
We should mention some of the other possible semantic relations, including (1) case relations, which are used in semantic graphs (cause, effect, agent, patient, etc.; see the corresponding chapter), what we will call (2) systemic relations (symbolic, semi-symbolic and semiotic relations; see the chapter on figurative, thematic and axiological analysis); and what we will call sign relations (a symbol, index, or icon of something).
2.4 CATEGORIAL / INCREMENTAL RELATIONS
All properties can vary according to the observing subject and time. The same applies to relations established between terms. This means that: (1) from one observer to another, different or even incompatible relations may be established between the same terms, rightly or wrongly; (2) the nature of the terms or their interaction may change over time; or (3) they can remain the same while the knowledge we have about them changes (a particular character may view particular terms as linked by a relation of identity, and then realize his mistake and change his mind). In a literary text, the observers can be the following, among others: the real or empirical author, the implied author (the impression that the text gives of its author), the narrator, the narratee, the character, the implied reader (the impression that the text gives of its expected and unexpected readers), the real or empirical reader. For details on this typology of observing subjects, see the chapter on thymic analysis.
2.5 DECIDABILITY, THE OBSERVING SUBJECT, AND TIME
All properties, relations or otherwise, are either decidable -- e.g., we may judge that two terms are identical -- or undecidable -- e.g., we may not be able to say whether two terms are identical or not.
Some relations are categorial: they either are or are not, with no possible intermediate position. For instance, in theory, two terms are either opposite or they are not; there is no possible intermediate position. Other relations may be considered from either a categorial or an incremental perspective. From a categorial standpoint, for example, there is a relation of mutual exclusion between two terms if and only if each time one of the terms appears, the other term is absent, and vice versa; from an incremental standpoint, there is mutual exclusion if this situation applies nearly always, usually or most of the time (the mathematical limit being half of the cases plus one. Thus, from an incremental perspective, a homologation does not fall apart because one of the elements of the opposition sometimes appears without its counterpart from the other opposition in the homology. Moreover, quantitative considerations are not the only ones, and in order to determine whether a relation is active or not, one must consider the quality, or significance, of the elements that express it.
2.6 THE STRUCTURE OF HOMOLOGATION
At least one other device beside homologation could rightfully have fit into this chapter on structures: the semiotic square (which deals with relations of opposition and implication). Instead, we have chosen to devote a separate chapter to the semiotic square, and here we will examine homologation in more detail. For another analysis with homologations in it, consult the chapter on figurative, thematic and axiological analysis.
2.6.1 HOMOLOGATION DEFINED
Homologation is the relation between (at least) two pairs of opposite elements, such that for two oppositions A/B and C/D, one can say that A is (usually or always) to B as C is (usually or always) to D8. The formal notation of a homology is written in the following manner: A : B :: C : D. For example, in our culture, white : black :: life : death :: positive : negative (white is to black as life is to death, as positive is to negative, and so on). The following notation can also be used: A / B :: C / D.
NOTE: SOME DIFFICULTIES WITH ANALYSES USING HOMOLOGATION
When identifying a homologized structure, there are some common pitfalls to avoid:
1. Uncoupling the terms in an opposition (such as life/positive :: death/negative instead of life/death :: positive/negative).
Inverting the relations between terms (such as positive/negative :: death/life instead of positive/negative :: life/death).
Bringing oppositions together without checking and demonstrating that there is homologation; in particular, concluding that an opposition Z is homologized with an opposition X just because Z is homologized with Y and Y is homologized with X.
4. Unintentionally using "compound oppositions", we might call them, whose terms define more than one opposition. For example, the pairs gain/loss or excess/lack would be preferable to a less precise opposition such as profusion/loss.
5. Unintentionally confusing synthetic approaches (e.g., governing the opposition cave/moon) and analytic approaches (governing the opposition low/high in which the objects cave and moon are participants). In other words, the homologation of characteristics (low/high) should not be confused with the indirect homologation of the elements that possess these characteristics (cave and moon).
2.6.2 THE CONSTITUENT RELATIONS OF HOMOLOGATION
We shall say that a relation of similarity is established between the terms of one opposition of a homology and the corresponding terms of the other opposition (between A and C and between B and D). In addition, a relation of qualitative analogical similarity is established between the two oppositions themselves. Lastly, a relation of simple or reciprocal presupposition is established between the corresponding terms. For example, there is a relation of simple presupposition if each time the theme of life comes up in a text, it is put in a positive light, but that other themes besides life are associated with a positive value. (In other words, life necessarily presupposes a positive value, but a positive value does not necessarily presuppose life). There is a relation of reciprocal presupposition between life and positive if life is positive and nothing else is. Furthermore, the association life-positive excludes the association life-negative, and the association death-negative excludes the association death-positive.
2.6.3 HOMOLOGY AND COUNTER-HOMOLOGY
We will use the term counter-homology for a homology that reverses the terms of one of the two constituent oppositions of a homology. For example, a text in praise of suicide values death and devalues life; it takes the opposite view from the usual homology, and transforms the homology life : death :: positive : negative into a counter-homology life : death :: negative : positive.
A homology and its counter-homology may belong to identical or different system levels. We will distinguish particularly between the following system levels for texts, and with adjustments for other semiotic acts, from the higher to the lower levels: (1) the dialect: the language system; (2) the sociolect: the usage of a dialect and other standards specific to a particular social practice (rather than a particular social group), which defines the discourses (literary, religious, etc.) and genres (novel, poetry, etc.) of semiotic acts; (3) the idiolect: the particular usage of a dialect, a sociolect and other, strictly idiolectal regularities, which defines the style of a producer. (4) the textolect: the particular usage of the three aforementioned systems and other, strictly textolectal regularities in a particular semiotic act (e.g., a particular text by a particular author); and lastly, (5) the analect: the elements of a semiotic act that don't come from any system. The minimal condition for a unit to be systematic in nature is to be repeated at least twice. For example, while a topos (or sociotopos) – such as being absent-minded from falling in love – is not a dialectal unit, it is found in at least two texts (or semiotic acts) by different authors. While an idiotopos is not a dialectal or sociolectal unit, it is a semantic unit found in at least two texts by the same author. While a textotopos is not a dialectal, sociolectal or idiolectal unit, it is repeated at least twice in a single text by a single author. An anatopos is a semantic unit that is found just once in a single text by a single author.
Homology and counter-homology are symmetrical categories. However, we can reserve the term "counter-homology" for marked homologies, i.e., less frequent ones (whether they come from the same system level as the homology or a different system level). For example, the homology virtue : vice :: positive : negative, which is very common in literature, has a counter-homology, virtue : vice :: negative : positive in libertine literature, particularly in the works of the Marquis de Sade.
3. APPLICATION: THE BATTLE OF ARGONNE BY MAGRITTE
The Battle of Argonne (1959) by Magritte brings together -- in a polemical manner, if we are to believe the title, which evokes a battle, or a group of famous battles of the first world war -- two opposite objects, as shown by the homologized oppositions presented in the table below. The characteristics listed in this table relate to a point of comparison (e.g., the characteristic "on the left" relates to the point "horizontal position")9. We were unable to obtain rights to post an image of Magritte's painting, in which there is a cloud on the left, opposite a levitating rock on the right.
The main homologized oppositions in The Battle of Argonne
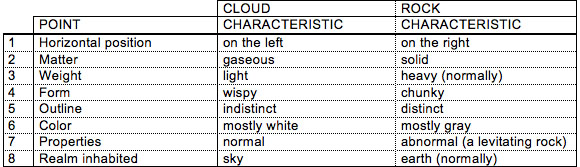
Although numerous oppositions keep the main figures of the painting far removed from each other, what paradoxically emerges from the comparison is the astounding overall resemblance between a cloud and a rock, simply from surrealistically suspending the heaviness inherent to the rock10. The results of the analysis depend on the objective and the degree of precision of the analysis. Since the objective was to identify and homologize oppositions, in order to increase the contrast between the two objects being analyzed, we have said that the rock is normally heavy and belongs to the earthly realm. These properties are virtualized in the painting -- neutralized, but not absent, as the surrealistic effect of the painting testifies -- in favor of the opposite properties in common with the cloud. Each time, we have selected the degree of precision most suited to our objective: for example, while a detailed analysis would classify the cloud as wispy and the rock as chunky, a more general analysis would view them as similar elliptical shapes.
The moon at the top of the canvas seems to be mediating between the cloud and the rock11 : for one, it is in a somewhat intermediate horizontal position; For another, it is simultaneously white on the left -- just as the cloud is generally white and located on the left -- and dark on the right (so dark that it merges with the sky) -- just as the rock is generally dark and located on the right. The moon and the rock have other shared properties: the moon is also a mass of levitating rock with an irregular surface; like the moon, and like the cloud on the canvas, this rock has a lit side (toward the earth) and a dark side (toward the sky). While the moon has only two levels of luminosity -- light and dark -- the cloud and the rock have three: actually, the part facing us has an intermediate level of light; In their luminosity, then, the cloud and the rock reproduce the triadic nature of the three-figured composition within themselves.
4. LIST OF WORKS CITED
- GENETTE, G. (1982), Palimpsestes, Paris: Seuil.
- GREIMAS, A. J. and J. COURTÉS (1979), Sémiotique. Dictionnaire raisonné de la théorie du langage, Paris: Hachette Université.
- HÉBERT, L. (2007), Dispositifs pour l’analyse des textes et des images. Introduction à la sémiotique appliquée, Limoges: Presses de l'Université de Limoges.
- HÉBERT, L. (2009), "Autotextualité, intertextualité, architextualité, autoreprésentation, autoréflexivité et autres relations apparentées", in L. Hébert and L. Guillemette (dir.), Intertextualité, interdiscursivité et intermédialité, Québec: Presses de l’Université Laval, pp. 71-78.
- HÉBERT, L. and L. GUILLEMETTE (2009), "Intertextualité, interdiscursivité et intermédialité", in L. Hébert and L. Guillemette (dir.), Intertextualité, interdiscursivité et intermédialité, Québec: Presses de l’Université Laval, pp. 1-9.
- RASTIER, F. (1989), Sens et textualité, Paris: Hachette.
5. EXERCISES
A. Identify the homology or the homologies present in: "Death is a sleep". Caution: If you identify multiple homologies, don't forget that every opposition must be homologized with every other; do not consider an opposition that cannot be completely homologized.
B. Use the following elements, listed in alphabetical order, to form oppositions, and place the terms so as to identify the series of homologies on which Traditional Chinese Medicine is based (source: M. Deydier-Bastide, Abrégé de médecine traditionnelle chinoise, Désiris, 1997, p. 21): low, hot, light, femininity, cold, high, diffuse, stillness, masculinity, movement, dark, solid, Yang, Yin.
1 This text represents a complete revision and expansion of the first chapter of our book, Tools for text and image analysis (Hébert, 2007).
2 Oppositions are not always dyadic, and one sometimes finds triadic and tetradic oppositions, among others; for instance, in French Canadian rural legend, the three following spaces form a triadic opposition: forest / countryside / city (see the chapter on figurative, thematic and axiological analysis).
3 Can we consider a non-directional relation to be equivalent to a bidirectional relation? Probably not. Admittedly, if A is linked to B, this implies that B is linked to A; but, to use an electrical metaphor, this simply means that the terms are in contact, not that there is necessarily any "energy" running through this contact in either direction.
4 Alternation is a relation of mutual exclusion in which one of the terms must necessarily be present (the absence of all the terms is excluded); the terms are said to be alternating. We will give an example involving two terms, but remember that an alternation can involve more than two terms: in a realist text, if a human being cannot be alive and dead at the same time, (s)he must be one or the other.
5 As for simple presupposition, it can be seen as a correlation that is categorial (the element's presence has a status of 0 or 1, with no other possibility) and asymmetrical (operating in just one direction).
6 We will give a simple example of generative and genetic viewpoints: If we isolated the world view governing the production of a work of literature, we would be isolating a hypothetical, abstract form that generated the work; if we studied the notes and the rough drafts for this work, we would be looking from a genetic viewpoint.
7 Greimas and Courtés (1982, p 259) distinguish four types of "références": (1) those established within the utterance (e.g., in syntactic anaphorae ("he" anaphorizing "soldier" in "The soldier stood up. He took my hand.") and semantic anaphorae ("do" anaphorizing "sew" in "Are you going to sew it? -- Yes, I'll do it."); (2) those established between the utterance and the enunciation (through deictics); (3) those existing between two discourses (for which they suggest the term "intertextuality" instead); (4) those established between the utterance and the natural world. Certainly a more suitable term to encompass these various unidirectional and other relations is "referral" [Fr. "renvoi"]. One of the acceptations for the [French] term "référence" seems to correspond to Greimas and Courtés' fourth type of reference, but not all theories of reference view it or view it exclusively as referring to the objects of the natural world. For référence [Fr.] strictly speaking, we can use the term "reference" or, to avoid polysemy, the term "referentiation".
8 According to Greimas and Courtés (1982, p. 144), in a homologation, the relation between A and B on the one hand, and between C and D on the other, "is identical and can be recognized as one of the elementary logical relations (contradiction, contrariety, complementarity)". For example, if I say that life is to death as not-life is to not-death, the relation between the two oppositions is contradiction. It is at least clear that homologation has as its basis a relation of similarity between the corresponding terms of each opposition and between the oppositions themselves. According to Rastier (1997, p. 38): "Matrices of homologation play an eminent role in the methodology of the social sciences (in Dumézil and Lévi-Strauss, for example): they found in fact qualitative analogical reasoning". We should add that quantitative analogical reasoning is most rigorously manifested in the mathematical proportions that make the rule of three work (e.g., 10 is to 100 as 100 is to 1000).
9 In logical terms, a point is a subject (what we are talking about) to which we apply a characteristic, which is a predicate (what we are saying about the subject); a characteristic and the point to which it relates together form a predicate applied to a subject, which here is the cloud or the rock. The relation between the compared object and a point of comparison is a mereological relation, more precisely, a relation between a whole (e.g., the cloud) and one of its parts (e.g., its horizontal position).
10 The painting can be viewed as a rhetorical figure: metaphorical comparison; note that a commonly used function of comparison, especially surrealistic comparison, is to bring out the previously unnoticed resemblance between two very disparate elements.
11 This mediation by the moon may be compared to that of the bottle-carrot present in another of Magritte's works, The Explanation (1952). It is analyzed in the chapter on the semiotic square.