You are here : Home Page / Theories / Semiotics of Rhythm

A Little Semiotics of Rhythm. Elements of Rhythmology

1. Abstract

Three operations are needed to produce a rhythm: a segmentation into units, and the arrangement and seriation of the units. "Arrangement" also designates the component that concerns the arrangement of the units in a temporal and/or spatial range. Rhythm can be defined as the specific configuration produced by combining at least two units of identical (A, A) or different (A, B) "value" in at least two positions that follow one another in time.

Rhythmic analysis takes the following principal factors into account. 1. The number of successive positions in the rhythmic sequence. For example, a quatrain is a grouping of four lines, and an alexandrine is a grouping of 12 syllables. 2. The number of simultaneous positions in the rhythmic sequence. The number of simultaneous positions defines the planarity of sequence. If there is no simultaneous position possible, the rhythm is monoplanar; otherwise it is pluriplanar (or polyplanar). For example, a line and a stanza are monoplanar sequences relative to syllables and lines, respectively: a single syllable or a single line occupies one relevant position in the succession. 3. The number of units per successive position (including potential superposed units). For example, a quatrain is arranged with one line per position; an alexandrine is arranged with one syllable per position. 4. The number of units that can occupy each position. This does not mean the number of units per successive or simultaneous position, but the number of different units from which one can select to occupy the successive or simultaneous position. In order to represent a rhythmic pattern, each different kind of unit can be represented with a different letter. For example, A and B could represent the two rhymes of a quatrain in a sonnet. 5. The organization of the pattern. With respect to what type of succession of units occurs, the major organizational patterns are: (1) immediate succession (e.g., A, B) and (2) mediate succession (e.g., between A and B in: A, X, B, where X = silence; however, there is immediate succession between A and X and between X and B). With respect to how the different kinds of units are ordered, the major organizational patterns are: (1) grouping (e.g., A, A, B, B); (2) interlacing (e.g., A, B, A, B); (3) embedding (e.g., A, B, B, A). 6. The type of units involved. Rhythms are not restricted to the so-called "temporal" semiotics, like music, film, and literature. Rhythm, then, is not a characteristic solely of poetry, nor solely of versified poetry. In order to have rhythm, all that is needed is at least two units strung together (even if it is the same unit, reapeated) in at least two successives positions. 7. The actual units involved. The actual units involved are the tokens of the types of units involved, e.g., a particular seme or a particular phoneme used in the rhythmic sequence. For example, in a particular quatrain of a sonnet, the rhymes may be –our (A) and –aine (B). 8. The duration of the units. With respect to the length of its lines, a stanza of alexandrines is isometric (and thus monometric): it contains units that always have 12 syllables.

2. THEORY

Rhythm is a complex notion. What we will present here is not a scholarly synthesis on the subject. Our objective is simply to offer some avenues for analyzing rhythm and the arrangement it presupposes.

2.1 ARRANGEMENT AND RHYTHM

Three operations are needed to produce a rhythm: a segmentation into units, and the arrangement and seriation of the units.

These units can be strictly semiotic:

1. The signifier (or its parts, e.g., the phonological features of the phonemes: vowel, consonant, open, closed, etc.);
2. The signified (or its parts, such as semes and cases, e.g., the semes /liquid/ and /edible/ in the signified 'water', or groupings of these parts: isotopies, semic molecules, etc.);
3. The sign (i.e., the combination of a signifier and a signified, e.g., the word "water").

The units can also be peri-semiotic:

4. The stimulus to which a signifier refers (e.g., a particular phone, i.e., a specific utterance of a phoneme; or a particular phonic feature);
5. The mental image (or multimodal simulacrum (Rastier)) that a signified defines (e.g., the representation of a pet fish created by the syntagm "the canary and the fish"; or a particular representational feature).

Lastly, the units can be mixed, at least in theory (stimulus and signifier, simulacrum and signified, etc.).

Rastier uses the term distribution (2001, p. 249) for the textual component relating to the arrangement of the units of the linguistic signifier, and the term tactics (1989) for the component relating to the arrangement of the units of the linguistic signified¹. These names can be extended to non-linguistic signifiers and signifieds. We can have an arrangement of stimuli and an arrangement of representations (or mental images). Arrangement can then be viewed as the overall component relating to the arrangement of semiotic and peri-semiotic units in a temporal and/or spatial range. The propositions we advance are in the context of arrangement, and are therefore an indirect contribution to distribution and tactics.

The various specific arrangements (distribution, tactics, etc.) must be distinguished because the way they are segmented does not exactly correspond. We will give just a few instances of non-correspondance. For tactics and distribution, one signified may be distributed over multiple elements of the signifier (e.g., the signified 'water' distributed over five graphemes: w, a, t, e and r). One signifier may be associated with multiple signifieds, particularly with symbolic connections, which "superpose" a "literal" signified (flower with the signified 'rose') and a "figurative" signified (flower with the signified 'woman'). Linguistic signifiers have two distributions: one for the phonemic signifiers and one for the graphemic signifiers (whose associated stimuli are the graphs, i.e., the letters indicating the graphemes). These two distributions do not coincide exactly; for example, one phoneme may be associated with more than one grapheme, such as the phoneme [o] and the graphemes e-a-u).

Succession may occur in time only, or in time and space, such as a succession of elements in a table that is read, say, from left to right. Going beyond the rough distinction between semiotics of space and semiotics of time, we will distinguish semiotics or languages: (1) of constrained time and consecution: e.g., a film screening is generally not interrupted, slowed down, accelerated, run backward, etc.; (2) of unconstrained time with constrained consecution: a text is generally read from one word to the next, but one can take a break between two words, go back, skip ahead, etc.; (3) of unconstrained time and consecution: e.g., one can look at a painting for as long as one chooses, and go from certain figures in it to others at will.

2.2 A DEFINITION OF RHYTHM

Rhythm can be defined as the specific configuration produced by combining at least two units of identical or different "value" in at least two positions that follow one another in time. With respect to this definition, the minimal rhythmic configuration – two units placed in two successive positions – will take one of the following four forms: (1) A, B; (2) B, A; (3) A, A or (4) B, B².

In this minimal rhythmic configuration, the value used, one of the two values used, or both values (in some cases, the silences will be of different kinds) may be a "semiotic silence", i.e., the absence of a "full" unit. Considering the four preceding forms again, if we assign a semiotic silence to B, then we will have: (1) A, ∅; (2) ∅, A; (3) A, A or (4) ∅, ∅.

If a moment in a rhythmic sequence can take the form of the fourth configuration, e.g., the two silences between two words separated by a double space (A, ∅, ∅, B), what would it be like to have a semiotic production based entirely on this configuration? First, we have to realize that semiotic silence is never absolute; so our double space between two words is not the vacuum of space or the absolute void between atomic particles, but simply the lack of a letter. Imagine a painting whose white canvas is simply divided in two by a vertical line. From left to right there will be a temporalized succession of two lacks of paint (the line is thought of as a non-stripe and a non-pigment). "Time" elapses, something happens (it's not an absolute semiotic silence), but the expected phenomena (of pigmentation) do not occur.

We are not defining rhythm restrictively as the same elements returning. This way we can be sure we do not exclude from rhythmic analysis rhythms that are partially repetitive (e.g., A, B, A, C) and rhythms that are entirely non-repetitive (e.g., A, B or A, B, C), alongside the rhythms that are entirely repetitive (e.g., A, A or A B, B, A), as far as the inventory of units is concerned.

2.3 FACTORS OF RHYTHM

The inventory of rhythmic patterns -- even the general ones -- is certainly vast. Rhythmic analysis takes the following principal factors into account, which we will explain in detail afterwards.

1. The number of successive positions in the rhythmic sequence. For example, a quatrain is a grouping of four lines, and an alexandrine is a grouping of 12 syllables.
2. The number of simultaneous positions in the rhythmic sequence. The number of simultaneous positions defines the planarity of sequence. If there is no simultaneous position possible, the rhythm is monoplanar; otherwise it is pluriplanar (or polyplanar). For example, a line and a stanza are monoplanar sequences relative to syllables and lines, respectively: a single syllable or a single line occupies one relevant position in the succession.
3. The number of units per successive position (including possible superposed units). For example, a quatrain is arranged with one line per position; an alexandrine is arranged with one syllable per position.
4. The number of units that can occupy each position. This does not mean the number of units per successive or simultaneous position, but the number of different units from which one can select to occupy the position. This number can be a priori open or closed. In order to represent a rhythmic pattern, each different kind of unit can be represented by a different letter. For example, A and B could represent the two rhymes of a quatrain in a sonnet.
5. The organization of the pattern. With respect to what type of succession of units occurs, the major organizational patterns are: (1) immediate succession (e.g., A, B) and (2) mediate succession (e.g., between A and B in: A, X, B, where X = silence; however, there is immediate succession between A and X and X and B). And with respect to how the different kinds of units are ordered, the major organizational patterns are: (1) grouping (for example, A, A, B, B); (2) interlacing (for example, A, B, A, B); and (3) embedding (for example, A, B, B, A). In a tetradic rhythmic pattern (four units) with two values (A and B), like that of the rhymes in a quatrain of a sonnet, these three major organizational patterns correspond respectively to 1) couplet rhymes (A, A, B, B); 2) cross rhymes (A, B, A, B); and 3) envelope rhymes (A, B, B, A).
6. The type of units involved. As for the types of semiotic productions in which they occur, rhythms are not restricted to the so-called "temporal" semiotics, like music, film, and literature. Thus rhythm is not solely a characteristic of poetry in particular, nor just of versified poetry. In order to have rhythm, all that is needed is at least two units strung together (or even the same unit reapeated) in at least two successives positions. So it makes perfect sense to talk about rhythm in a pictorial work.
7. The actual units involved. The actual units involved are the tokens of the types of units involved, e.g., a particular seme or a particular phoneme used in the rhythmic sequence. For example, in a particular quatrain of a French sonnet, the rhymes may be –our (A) and –aine (B).
8. The duration of the units. Times and rhythms can be: (1) isometric: all of the units have the same range (de facto or by "rounding" to standard values); (2) allometric: all the units have different ranges; or (3) parametric: some units have the same range and others do not. Isometric times and rhythms are necessarily monometric. Allo- or parametric times and rhythms are necessarily polymetric. With respect to the length of its lines, a stanza of alexandrines is isometric (and thus monometric): it contains units that always have 12 syllables; a stanza alternating between dodecasyllabic lines (alexandrines) and octosyllabic lines (eight syllables) would be parametric (and thus polymetric). We can distinguish major cadence rhythmic sequences and others in minor cadences. The latter use longer and longer units in their succession; the former use shorter and shorter units.

2.4 DISCUSSION

2.4.1 THE NUMBER OF SUCCESSIVE POSITIONS

The structures produced by the succession of positions can be short, medium, or long; dyadic, triadic, etc.; even or odd; and so forth. Each of these structures has its own potential aesthetic effects. For example, odd rhythms create an effect of asymmetry, instability and/or dynamism, at least if they are short enough that the odd rhythm can register. If the sequence is monoplanar, the number of successive positions is also the number of units that form the sequence (including possible silences).

2.4.2 THE NUMBER OF SIMULTANEOUS POSITIONS

A rhythm is monoplanar if it uses only one unit in each position: e.g., A, B, C. A rhythm is pluriplanar if it uses more than one unit in each position: e.g., A, B+C, D. If it uses two units per position, it will be described more precisely as biplanar; if it uses three, triplanar, etc. Obviously, a rhythm can be partially monoplanar and partially pluriplanar, i.e., monoplanar in one or more parts of the rhythmic sequence and pluriplanar in one or more other parts.

The term homoplanar will be used to describe rhythms whose planarity does not change along the way (e.g., whose rhythm is biplanar from the beginning to the end of the rhythmic sequence). And the term heteroplanar will be used to describe rhythms whose number of planes changes along the way (e.g., monoplanar in one place and pluriplanar in another; or biplanar in one place and triplanar in another).

The signifiers of language (except for special phemomena such as simultaneous replies in theater or in Altman's films) always proceed from monoplanar rhythms, since a given signifier posistion cannot be occupied by more than one unit. For example, you don't find two graphemes in a position allotted to one grapheme, except in special cases.

NOTE: PLANARITY AND INTERPRETIVE PERSPECTIVE

We will distinguish three interpretive postures: presential (defined by a "window" that is moved from one position to the next), retrospective (e.g., at position 2, changing the status of position 1), and prospective (anticipatory, e.g., at position 1, anticipating what position 2 will be). Depending on the posture, the planarity may be modified. Take the sequence A, B+C, D. In the "interpretive present", it is initially monoplanar, then biplanar, then monoplanar. But from the second position, through retrospection, the first position becomes biplanar A+Ø, and through prospection (anticipation) the third position becomes biplanar as well, C+X (X would correspond to a value of some sort or a non-value, i.e., a silence).

2.4.2.1 NECESSARY AND ACCIDENTAL PLANARITIES

The planarity of a phenomenon with respect to a particular normative system or particular physical constraint will be either accidental or necessary (essential). The planarity is necessary if it cannot not occur. It is accidental if although it did occur, it could have been otherwise. For example, the monoplanarity of the linguistic signifier is necessary, since this signifier is linear, with no possibility of superposition (at least that is how it is understood and generally used). In contrast, the monoplanarity of the image in a particular film is accidental: the film could have superposed fade-in and fade-out images (during the entire film or just at certain moments).

A voluntarily silent contemporary film (with no sound track -- no words, music or noise) is accidentally monoplanar with respect to the relation between visual and auditory signs. Monoplanarity is then the result of a specific aesthetic vision (standard). But during the silent film era, this monoplanarity was necessary, since the sound could not be reproduced (a physical constraint).

NOTE: PLANARITY AND SYSTEM

The status accidental/necessary may vary depending on the systems involved. So it can also be said that our contemporary silent film is necessarily monoplanar if viewed in terms not of what was possible (according to film language in general, the system that we will call "lectal"), but in terms of what was done (this film's own system -- the textolectal system --, to which we will return later): The standard for this film dictated that no sound could be superposed on any images. For a typology of normative systems, see the chapter on structural relations.

2.4.2.2 TEMPORAL RELATIONS BETWEEN UNITS IN THE SAME SUCCESSIVE POSITION

The temporal relation between the formal units that are copresent in a single successive position can be: (1) strict simultaneity (in the diagram below, A and B); (2) partial simultaneity (C and D; only one of the four possible forms of partial simultaneity is shown in the diagram); (3) immediate succession (E and F, in particular); (4) delayed or mediate succession (which inserts a silence between the units, between G and H). For details on temporal relations, see the chapter on structural relations. All of the cases shown -- except strict superposition -- yield a different segmentation of units and positions; we will return to this question later, distinguishing the segmentation of rhythmic forms (units) from the segmentation of the rhythmic ground (positions).

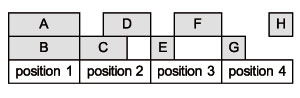
2.4.3 THE NUMBER OF UNITS PER SUCCESSIVE POSITION

If the rhythm is pluriplanar, then the number of units per successive position is greater than one (including potential silences). If the rhythm is monoplanar, then this number is equal to one.

A change in the grain of segmentation (in the size of the units produced by the segmentation) may change the planarity and thus the number of units per successive position. For instance, a syllable can combine multiple phonemes in a single syllabic position, of course; from this standpoint, there is pluriplanarity. But the fact remains that there is only one syllable in a single syllabic position and only one phoneme in a single phonemic position; from this standpoint, there is monoplanarity.

Consider this quote by Julien Gracq: "Écrivain ou plumitif, percheron ou pur-sang" ["Writer or pen pusher, draft horse or thoroughbred"], where "plumitif" signifies "hack writer" and "percheron" means "draft horse". If the grain of segmentation is the word, then the rhythm of the semes /positive/ (A) and /negative/ (B) is monoplanar and has four positions: A, B, B, A. Note that a rhythm may discard positions that do not contain the relevant units (in this case, the positions defined by the word "or"), rather than recognizing them as bearing silences. If the grain is the syntagm (whose demarcation is the comma here), the rhythm of these same semes is biplanar and has two positions: A+B, B+A.

Consider this quote by Baudelaire (from the poem "Tout entière"): "Son haleine fait la musique, / Comme sa voix fait le parfum" [Her breath makes music, / And her voice makes perfume"]. If the grain of segmentation is the word, and one counts only the nouns, the rhythm of the semes /smell/ (A) and /hearing/ (B) is monoplanar and has four positions: A ("breath"), B ("music"), B ("voice"), A ("perfume"). If the grain of segmentation is the line (whose demarcation is the slash here), the rhythm of these same semes is biplanar and has two positions: A+B, B+A. This is not a chiasmus, since it does not matter in which order the As and the Bs appear in each line; each line creates a simultaneity of As and Bs.

This issue of how variations in segmentation affect the analysis is a broad one; it does not apply just to analysis of rhythms, but to any analysis that involves an arrangement, and more generally, to any analysis that involves wholes and parts. For details, see the chapter on thymic analysis.

2.4.4 THE NUMBER OF UNITS THAT CAN OCCUPY EACH POSITION

The number of units from which one can select may be essential (defined a priori, e.g., in classical French poetry, a rhyme is necessarily feminine or masculine), or conversely, it may be accidental (a priori somewhat open, e.g., the color of the vertical stripes of color in a painting, or the choice of a phoneme in a phonic poem). Whether it is an open or closed "paradigm" (the pool of units from which one draws to produce a rhythmic sequence), once the sequence is completed (with the exception of potential infinite rhythmic sequences), it is possible to establish the inventory of the various units that were used (and the various units that were not used). For example, a traditional sonnet will employ only five rhymes (A, B, C, D, E). To give another example, a painter can theoretically choose from thousands of colors, but his striped painting will only use three, and thus in each stripe of the painting, he has in a way chosen from three colors.

When one calculates the number of units or values that can occupy a position, one must define whether one of these values can be a "silence", i.e., the absence of a full value. For example, when counting syllables in lines of poetry, there is no silence possible; there has to be one (and only one) syllable in each position. On the other hand, in a film, the music can appear at the beginning and end of a sequence, for example, but be absent in the middle, creating the rhythm: music, silence, music (A, Ø, A).

2.4.4.1 VARIATIONS IN THE INVENTORY OF UNITS

At a given point in a rhythmic sequence, the next unit will be either the same as the previous one (A → A; the arrows here separate successive units), or it will be different (A → B). If the units are quantitative, the next unit will be an increase over the previous one (100 → 150; a little → a lot), a decrease (100 → 50; a lot → a little), or a continuance (100 → 100; a little → a little). Whether the units are qualitative or quantitative, if the next unit is different, it will be either a unit already present in an earlier position (A, B → A), or a new unit (A, B, → C). In the first instance, the variety of the inventory is kept the same (two different units in our example, A and B); in the second instance, the variety of the inventory of values has just expanded, and there will be an addition to (or increase in) the variety of the inventory (three different units in our example: A, B, C).

2.4.5 ORGANIZATION OF THE PATTERN

Above we presented three main rhythmic patterns -- grouping, embedding, and interlacing -- and illustrated them with dual-value (A and B) tetradic rhythms, respectively: A, A, B, B; A, B, B, A; and A, B, A, B. But we must remember that these main patterns also apply to non-tetradic rhythms, and rhythms other than those with two values; that they can be combined and can be applied not just to units, but to groups of units, and that a single unit in a sequence can proceed from multiple patterns. Here are some of the many examples of patterns:

1. A, A: grouping (minimal grouping);
2. A, A, A, A, A: grouping;
3. A, B, B: grouping;
4. A, A, B, B, C, C: grouping (of As, Bs, and Cs) and embedding (of the group of Bs);
5. A, B, C, A, B, C: interlacing (with not two, but three values: A, B and C);
6. A, B, A : embedding (minimal embedding, as embedding requires at least one unit surrounded by at least two identical units);
7. A, B, A, B, C, C: interlacing (of As and Bs, minimal in this case, since interlacing requires at least four units, and then two values at most) followed by a grouping (a minimal grouping of Cs);
8. A, B, B, A, A: embedding and grouping (of the As at the end of the sequence).

2.4.5.1 OPERATIONS FOR TRANSFORMING PATTERNS

The major operations of transformation are applied to one or more source elements in order to obtain one or more target elements. Target and source elements can correspond to types (models) or tokens (more or less complete manifestations of the model). Operations can occur: (1) within a token; (2) within a type; (3) from a type to its token; (4) from the token to its type; (5) from one token to another (of the same type or of a different type); (6) from one type to another.

The major operations of transformation are (the arrow separates the source elements and the target elements):

1. Addition (example: A, B → A, B, C);
2. Deletion (example: A, B, C → A, B);
3. Substitution (example: A, B, A, B → A, B, A, C);
4. Permutation (example: A, B, C → C, A, B);
5. Continuance (example: A, B → A, B).

It will serve our purpose to provide just a few details on these operations. For further discussion, see the chapter on transformational operations.

We will distinguish simple addition (e.g., A, B → A, B, C) and reduplicative addition (or repetitive addition). Reduplicative addition adds one or more units that are already present elsewhere. It can be partial (e.g., A, B → A, B, A) or complete (e.g., A, B → A, B, A, B).

We will distinguish partial deletion (e.g., A, B → A) and complete deletion (e.g., A, B → Ø). Complete deletion produces semiotic silence, and as such, is always relative.

We will distinguish any permutation (A, B, C → C, A, B) and permutation by inversion (A, B, C → C, A, B). If multiple units are permuted, this permutation can be seen as the result of permuting single units, or one or more permutations of blocks of units (A, B, C, D → C, D, A, B).

Note that by broadening and clarifying a notion of Rastier's (1987, p. 83), we are adding continuance to the four operations defined by the Mu Group (1982, p. 45-49; Klinkenberg, 1996, pp. 259-361). Unmarked continuance occurs when a unit that can be transformed is not. Marked continuance -- the kind that interests us -- occurs when expected transformations do not occur (since expectations may or may not be based on standards).

Additions / deletions of successive units result in the following correlative operations, respectively:

1. Expansion / condensation (range);
2. Lengthening / shortening (the passage of time);
3. Deceleration / acceleration (speed);
4. Lateness / earliness (expectation).

For example,in the sequence A, B, C, D, A, D, the A, D is a shortened version of the A, B, C, D that precedes it, and the D appears ahead of time due to the deletion of the expected intervening B and C. Note that permutation can produce lateness / earliness.

Rhythmic expectations may or may not be met. For example, an expectation of the chiasmus A, B, B, A is created after A, B, and is met when B, A comes. Conversely, rhythmic expectations are not met when A, C replaces A, B in A, B, A, B, A, C; or when A replaces F in A, B, C, D, E, A. Expectations produce an "image" (with the status 'possible') of the structure that will be realized (with the status 'real') if the prediction is right. An expectation that is met does not necessarily produce aesthetic euphoria: one could be hoping for the prediction to be wrong. An expectation that is not met does not necessarily produce aesthetic euphoria.

As we have said, operations occur between a source pattern and a target pattern, and these can have the status of type or token. We will give a few examples. The type pattern can simply be kept as is in the token (or from a different point of view, perfectly reduplicated in the token): a particular text might manifest a perfect chiasmus (A, B, B, A). But the type pattern can also be transformed in its token: in A, B, C, B, A, the C can be seen as a delaying element inserted into a chiasmus. The token can be seen as the site of an internal transformation operation: for example, a particular token chiasmus can be seen as the result of a reduplicative addition through reverse permutation (the A, B is followed by the B, A). Clearly, operations can act between a type pattern and another type pattern. For example, groupings (e.g., A, A, B, B) can be seen as the result of a permutation starting from an embedding (the two Bs are simply permuted with the second A in the source pattern A, B, B, A).

2.4.5.2 CIRCULAR AND LINEAR PATTERNS

A circular pattern ends the way it begins (e.g., A, B, A or A, B, A, B). A linear pattern does not end the same way it begins (e.g., A, B, C). A pattern can be partially circular, and thus partially linear (e.g., A, B, A, C). The beginning and the end used to determine circularity vs. linearity can each be composed of one unit (e.g., A and F in A, B, C, D, E, F) or a group of units (e.g., A, B, and E, F in A, B, C, D, E, F). So A, B, A, C is linear if we use a single unit to evaluate its status (A and C are different), and partially circular if we use two units to do this (A, B is approximately repeated by A, C).

2.4.6 THE TYPE OF UNITS INVOLVED

As far as the type of units concerned, rhythms are not restricted to signifiers (e.g., phonemes or graphemes) and the physical stimuli associated with signifiers (e.g., a particular phone (concrete utterance of a phoneme)).

Consequently, purely semantic rhythms, in particular, do exist. For example, as we saw, the four nouns in the utterance "Writer or pen pusher, draft horse or thoroughbred" form an embedded semantic rhythm (A, B, B, A) with the semes /positive/ (A), /negative/ (B), /negative/ (B), /positive/ (A).

The units involved in a rhythm can be qualitative. But they can also be quantitative and establish extensities or intensities of elements. Remember that the quantitative -- i.e., the measurable -- is divided into two subcategories: firstly, extensity, which is measurable and countable (e.g., 1, 2, 3, etc.); secondly, intensity, which is measurable and not countable (uncountable) (e.g., not any, a little, average, a lot, etc.; none, minimal, low, medium, high, maximal, etc.). For more on this subject, see the chapter on the tensive model. For example, in traditional French versification, one analyzes the arrangement of tonic accents based on intense units. In the chapter on the tensive model, we proposed a typology of curves of euphoric intensity with three levels of intensity and three successive positions, with the curves defining as many rhythmic patterns.

NOTE: QUALITATIVE AND QUANTITATIVE VALUES

If the variety of quantitative values is reduced (at the outset or after rounding), these quantitative values also become qualitative values in some sense, for example, in a rhythm that combines only 500s (A), 1000s (B), 1500s (C) and 2000s (D), and not, let's say, 400 different values that vary between 0 and 2000. It is possible to convert extensity to intensity: for example, the value 50 or the range 50-99 = very low intensity (A); 100 or 100-199 = low intensity (B), etc. It is also possible to convert intensity to extensity: for example, low = 1, medium = 5, high = 10.

2.4.7 THE ACTUAL UNITS INVOLVED

The relations between the different units involved are not restricted to identity (between A and A, for example) and alterity (between A and B, for example). The relation can be opposition, e.g., the alternation between masculine and feminine rhymes in traditional French versification. An oppositional relation can be represented as a sequence of the type A, B, or of the type A, -A (where the minus sign indicates negation). The relation can also be similarity. For example, Baudelaire's poem "L'irréparable" is composed of stanzas in which the first and last lines are either identical or very similar, yielding the sequence: A, A’’; B, B’; C, C; D, D’’; E, E; F, F’’; G, G; H, H’; I, I’; J, J’’. We are distinguishing two degrees of similarity: the single apostrophe (') indicates a mere difference in punctuation; The double apostrophe (") indicates a lexical, syntactic, or other difference. For details on comparative relations, see the chapter on structural relations.

2.4.8 THE DURATION OF THE UNITS

2.4.8.1 INDICATING DURATIONS

Allo- and parametric times and rhythms may be factometric: the range of the units is derived by multiplying by one or more given factors (whole numbers, such as 2, 3, non-whole numbers, such as 1.2, 3.5). For example, A might last one second and B two seconds; The factor is then 2 (B = 2 x A) or 0.5 (A = 0.5 x B).

The ranges whose factors are whole numbers can be indicated by cumulating symbols (or by multiplying them by the factor). For example, AA, B, C (or 2A, B, C) indicates not that there are two A units, but that this unit has a double duration. The factors that are not whole numbers can be indicated directly in the rhythmic pattern, e.g., 3A, 2B, ½C

By methodological reduction (i.e., intentional, made explicit, and justified) an analysis can be restricted to the qualitative data. For example, the pattern: 3A, 2B, ½C would become A, B, C.

The empty set symbol (Ø) can be used to indicate silence. In order to indicate potentially different kinds of silences, one can use the end-of-alphabet variables, like X, Y, Z. To indicate the range of the silences, the conventions we have already presented can be used; for example, A, XX, B, X, C indicates that the interval of silence between A and B is twice as long as the one between B and C.

2.4.8.2 FOUNDATIONAL AND FORMAL RANGES

We will distinguish between two ranges that are operative in rhythm: (1) the range (temporal duration and/or spatial length) of the units that are strung together to produce the rhythm; (2) the range of the intervals of the temporal or temporalized ground against which the forms constituted by the units stand out.

Foundational time, like formal time, can be isometric, allometric, or parametric. But foundational time is often, even usually, isometric: it founds the regularity upon which formal temporal irregularity stands out when it is present.

In some cases, the range of the formal units can define the segmentation even of the temporal ground, and then there is no need to distinguish the two temporalities. In other cases, the segmentation produced by the range of the sequenced units and that produced in the temporal ground do not fully correspond, and it is helpful to distinguish these two segmentations.

Ultimately, the metric of the units can be established internally, by comparing the relative ranges of the units, or externally, in relation to a different metric whose grain might describe the ranges of the units perfectly (possibly by "rounding") or not so perfectly. This different metric can be temporal, and might be measured in seconds, or it can be spatial and might be measured in centimeters or pixels, for example.

Suppose that the metric ground is integrated into the actual semiotic production³. For example, the stripes in the picture we created below are the foundational rhythm. The stripes of paint on the painting by Molinari that we will analyze later are the formal rhythm and the foundational rhythm simultaneously. Or the metric ground may be solely in the "reading", or interpretation, of the sequence (e.g., if one uses a ruler or a chronometer to measure the range of the units).

If the metric ground is found in the actual work and is distinct from the temporality of the forms therein, then the rhythm is biplanar: units overlap one another, and therefore two rhythms are superposed. But not every polyplanar rhythm separates its rhythms into formal rhythms and foundational rhythms.

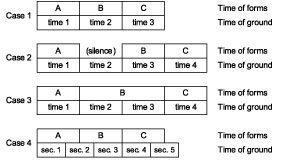
Suppose we have a rhythmic sequence A, B, C.

• Case 1. If the units have the same range, and they are not separated by one or more silences, there is no need to distinguish the range of the units from the range of the positions provided in the temporal ground, as the two articulations -- that of the units and that of the ground -- are identical. (See, for example, the painting by Molinari that we analyze later).
• Case 2. However, if a silence occurs, say between A and B, and we want to take this variable into account, then it becomes necessary to distinguish the time of the forms from that of the ground. Then the pattern becomes: A, X, B, C (X = silence, with the same range as the actual values).
• Case 3. Additionally, if one unit lasts longer than another, and we want to take this variable into account, then it becomes necessary to distinguish the time of the forms from that of the ground. Then the pattern becomes: A, BB, C (BB = double duration).
• Case 4. Now suppose that the units have the same range, that they are not separated by silences, that we want to relate these ranges to standard seconds, and that the units do not each last exactly a second (e.g., a second and one-half). The grains of the two temporalities are then different; they are allomorphic, and it is helpful to distinguish them.

The following diagram illustrates these cases.

Let's take a simple, concrete example. A canvas is separated into 10 vertical stripes of the same width. A rectangle (unit) has been set in each stripe. Each unit has the same height, but not necessarily the same width. Some units (A) are of the same width as the stripe; others (B) are only half as wide; others (C) are only a quarter as wide. The rhythm is then factometric. The stripes of the painting are the foundational time. The rectangles are the formal time. From left to right, the series of rectangles forms this rhythm: A, B, B, A, A, C, B, B, A, A. This sequence is represented in the diagram below (we have alternated the height of the position of the rectangles to aid comprehension, but we do not consider this as a biplanar rhythm).

Example of a canvas with ten stripes

If we take the duration of the units into account, the rhythm is more precisely: AAAA, BB, BB, AAAA, AAAA, C, BB, BB, AAAA, AAAA or, using a different convention, 4A, 2B, 2B, 4A, 4A, C, 2B, 2B, 4A, 4A. If we now include the silences (X), taking the silence to be the difference between the width of the stripe and the width of the rectangle inside it, we have: 4A, 2B, 2X, 2B, 2X, 4A, 4A, C, 3X, 2B, 2X, 2B, 2X, 4A, 4A. Note that the stripes could have been different sizes, producing an allometric foundational time; and the rectangles could have been identical in size.

3. APPLICATIONS

3.1 APPLICATION I: GREEN-RED SERIAL MUTATION BY GUIDO MOLINARI

We will present a partial analysis of the rhythmic sequence in the painting Green-Red Serial Mutation (1966) by the Québecois painter Guido Molinari (1933-2004)⁴. The artist was aware of the possible rhythmic interpretations of his paintings, judging from the titles of others of his works that contain "rhythm", e.g., the similar painting, Bi-Yellow Rhythmic Mutation (1965).

The painting has an arrangement of 24 vertical stripes of the same width (despite what the reproduction leads us to believe), which constitute the formal and foundational rhythmic units simultaneously. Note that the structure is fairly uniform on the vertical axis, which makes it so that there is notable rhythm only horizontally, and not vertically, or diagonally, or otherwise.

One can see that the artist chose an even structure, so there is no central unit; the axis of symmetry falls between two stripes. Traditionally, even structures are said to produce an effect of symmetry-stability-statisme, and odd structures an effect of asymmetry-instability-dynamism. Clearly, none of these effects is a priori negative or positive; it is possible they will be given value, but only within a particular aesthetic (e.g., in Art poétique, Verlaine explicitly assigns value to long lines of odd-numbers of syllables). One can also see that the artist chose an even number that is particularly important in our culture (with its 24-hour day), rather than 16 or 22, for example.

Each stripe is the site where a choice is made between four colors, which we will call by their common names, green, red, blue, and orange. Notice that as complementary colors, green and red form an opposition; likewise for blue and orange. The painting's title gives preponderance to two of the colors: Green-Red Serial Mutation. But it is not certain that this intentional preponderance comes out in the analysis of the painting; at least, it is not certain that it is established at all analytical levels.

The painting is constituted by a fourfold repetition of a six-unit sequence: light green (lg), dark red (dr), orange (or), blue (bl), dark green (dg), light red (lr). The light/dark variation does not show up well on the reproduction of the painting that we have. Blue and orange are of a different stripe, shall we say, relative to green and red, since they they do not come in light and dark versions. However, the opposition at work between green and red can be found in some sense, since blue is a darker and more somber color than orange, which is lighter and brighter. If we use color intensity as a rhythmic criterion, we identify the following rhythm: l, d, l, d, d, l.

This rhythm is constructed by reduplicative addition, i.e., adding a second l, d to the first l, d, followed by an inverted reduplicative addition, with l, d becoming d, l. The second l, d and the d, l at the end of the sequence constitute a chiasmus. One can also take the view that the first l, d and the d, l constitute a delayed chiasmus, by virtue of the second l, d inserted in between. In terms of intensity, the series begins and ends "gently", and reserves its moments of intensity for the middle part (which is not entirely intense, since there is an l in it).

Note that the matrix structure alternates the two complementaries green and red at the beginning (the first stripe) and the end (the sixth stripe), but these two colors are the same strength (light), which attenuates the opposition and makes them sub-contraries. Actually, in terms of the intensity of the opposition, dark green and dark red can be seen as super-contraries (a strong opposition between tonic elements) and light green and light red can be seen as sub-contraries (a weak opposition between atonic elements) in a device with four positions: dg, lg, lr, dr. The opposition super-contraries / sub-contraries was proposed by Zilberberg (2005). It should be distinguished from the opposition contraries / subcontraries found in the semiotic square (see the chapter on the semiotic square).

Another rhythm occurs in the painting, which is that of the primary (1) and secondary (2) colors: 2, 1, 2, 1, 2, 1. This rhythm is produced by a double reduplicative addition of the sequence 2, 1. This interlaced rhythm is highly repetitive, but it is not circular, since it does not end the way it begins.

From stripes 5 to 8, one observes an alternating structure -- g, r, g, r -- and an embedded structure --- d, l, l, d. This combination is powerful because it plays off the complementaries, and is relatively subtle at the same time, because it varies between two shades of each color. Because of its resonance, it is tempting to see it as the generative structure of the painting; we saw that the title emphasizes red and green, after all. In some ways, this should be the structure that begins the painting, but the painting prefers to start (stripes 1 to 4) and end (stripes 21-24) with a weaker structure, reserving its power for parts in the "center".

The table below shows the main rhythmic structures in Molinari's painting.

APPLICATION II: AN EXCERPT FROM LE BOURGEOIS GENTILHOMME BY MOLIÈRE

Consider the following excerpt from The Bourgeois Gentleman by Molière, in which the succession of different speakers produces a rhythm. The context: Monsieur Jourdain's various tutors are each insisting on the superiority of their own discipline, and they come to blows.

"The philosopher flings himself at them, and all three [the fencing master, the dancing master, and the music master] start punching at him and go out fighting.

1. [A] MONSIEUR JOURDAIN – Monsieur Philosopher!
2. [B] PHILOSOPHY MASTER – Rogues! Scoundrels! Insolent dogs!
3. [A] MONSIEUR JOURDAIN – Monsieur Philosopher!
4. [C] FENCING MASTER – A pox on the beast!
5. [A] MONSIEUR JOURDAIN – Gentlemen!
6. [B] PHILOSOPHY MASTER – Impudent rogues!
7. [A] MONSIEUR JOURDAIN – Monsieur Philosopher!
8. [D] DANCING MASTER – The devil take the jackass!
9. [A] MONSIEUR JOURDAIN – Gentlemen!
10. [B] PHILOSOPHY MASTER – Villains!
11. [A] MONSIEUR JOURDAIN – Monsieur Philosopher!
12. [E] MUSIC MASTER – To the devil with the impertinent fellow!
13. [A] MONSIEUR JOURDAIN – Gentlemen!
14. [B] PHILOSOPHY MASTER – Rascals! Beggars! Traitors! Impostors!

They leave.

MONSIEUR JOURDAIN Monsieur Philosopher, Gentlemen! Monsieur Philosopher! Gentlemen! Monsieur Philosopher! Oh! Fight as much as you like. I don't know what to do, and I'll not spoil my robe to separate you. I would be a fool to go among them and receive some damaging blow."

In central portion of the excerpt is a rhythmic structure with respect to who is speaking, a structure whose organization can be revealed by using a letter to designate each speaker: A: Monsieur Jourdain; B: Philosophy Master; C: Fencing Master; D: Dancing Master; E: Music Master.

1. The number of successive positions. The structure contains 14 units (just as a sonnet contains 14 lines, for example). It is even, thus making it possible to have perfect symmetry, whether in the number and kind of units assembled (the kind of unit is shown by the letter), or just in the number of units. Note, however, that odd structures can also be symmetrical if they are organized around an axis of symmetry that is one unit, such as E in the following sequence: A, B, C, E, A, B, C).
2. The number of simultaneous positions. One can observe that in this excerpt, Molière chose a monoplanar rhythm by excluding simultaneities, which would have meant two or more characters speaking at the same time. This preserves the very classical "clarity" in the scene, despite the free-for-all. We should note that it is rare in classical theater to have characters speaking at the same time, especially if they are saying different lines.
3. The number of units per successive position. Each successive position has just one unit, since the rhythm is monoplanar.
4. The number of units that can occupy each position. Five different units are combined: A, B, C, D and E. Consequently, in a completely free combinatorics, each of these units could have in theory occupied each position.
5. The organization of the rhythmic pattern. The rhythmic pattern is obtained by combining three occurrences of the (even) structure A, B, A, Y, followed by half of this structure (A, B), where Y is a variable equal to C first, then D, then E. This yields: A, B, A, C (Y = C) ; A, B, A, D (Y = D) ; A, B, A, E (Y = E) ; A, B.
   This organization seems to follow a certain logic: each line spoken by the philosopher is followed by a line from Monsieur Jourdain (the line is "Monsieur philosopher!", to be exact). Each line spoken by the other characters is also followed by a line from Monsieur Jourdain (the line: "Gentlemen!"). Despite appearances, Monsieur Jourdain's first line follows this logic, since it is a response to the last of the philosopher's lines in the preceding scene, a line in which the latter begins insulting his colleagues and then flings himself at them ("What! Rascals that you are ... "). This arrangement makes it so that Monsieur Jourdain says 7 lines, the philosopher says 4 (excluding the closing line from the preceding scene), and the other characters say one line each.
   Monsieur Jourdain's last line, with which he closes the scene, is a sort of condensation of the 14-element structure that precedes it. We actually find Jourdain's lines repeated as they were in the structure that precedes. Since a complete cycle of Jourdain's lines occurs when "Monsieur Philosopher!" is followed by "Gentlemen!", the last line of the scene contains two and a half cycles (the half cycle because it ends with "Monsieur Philosopher!" rather than "Gentlemen!"). Note that it ends with a half cycle, as does the 14-unit structure that precedes; this half cycle is the structure A, B (instead of A, B, A, Y) that ends the exchange with the other characters. Consequently, one could say that the last line is a micro-representation of the preceding structure.
   
6. The type of units involved. The units that create the rhythm are the speakers. There are other types of units present that create rhythms as well. For example, the content of the lines creates the rhythm: A, B, A, C, D, E, A, F, D, G, A, H, D, I (where A = "Monsieur Philospher!" and D = "Gentlemen!"). Note that all of the repeated lines are said by the "moderator" of the dispute, Jourdain.
7. The actual units involved. The speakers involved are: (A) Monsieur Jourdain, (B) the philosopher, (C) the fencing master, (D) the dancing master, and (E) the music master.
8. The duration of the units. Since we are not keeping track of the duration of the lines (in words, syllables, phonemes, or otherwise), the units have the same duration. That said, looking at actual duration, we should note that one of Jourdain's lines ("Gentlemen!") is distinctly shorter than the others (particularly in French), which are similar in duration.

4. REFERENCES CITED

BURNETT, M. (n.d.), "Molinari, Guido" [on line], in James H. Marsh, The Canadian Encylopedia. Web. 5 March 2011. http://www.thecanadianencyclopedia.com/index.cfm?PgNm=TCE&Params=A1ARTA0005365

RASTIER, F. (1989), "La tactique", Sens et textualité, Paris: Hachette, pp. 95-102. (reproduced on: http://www.revue-texto.net/1996-2007/Parutions/Parutions.html, “Trésors” tab)

RASTIER, F. (2001), Arts et sciences du texte, Paris: Presses universitaires de France.

RASTIER, F. (in press), "Rimbaud, Marine – Formes et rythmes sémantiques", in C. Koenig and P. J. de la Combe (dir.), La lecture insistante. Autour de Jean Bollack.

GROUPE µ (1982), Rhétorique générale, Paris: Seuil.

KLINKENBERG, J.-M. (1996), Précis de sémiotique générale, Paris: Seuil.

RASTIER, F. (1987), Sémantique interprétative, Paris: Presses universitaires de France.

ZILBERBERG, C. (2000), "Les contraintes sémiotiques du métissage", Tangence, Rimouski (Québec), 64, autumn, pp. 8-24 [republished on the Web: http://www.erudit.org/revue/tce/2000/v/n64/008188ar.pdf]

ZILBERBERG, C. (2005), Éléments de sémiotique tensive, Limoges: Presses de l’Université de Limoges.

5. EXERCISE

Analyze the rhythm produced by the succession of concentric circles in Accélérateur chromatique (1967) by the Québécois painter Claude Tousignant (b. 1932).

¹ Tactics is one of the four components of textual signifieds, along with thematics, dialectics, and dialogics, according to Rastier. Tactics was set out in Rastier, 1989 and Rastier, to be published. For details on these components, see the chapter on semic analysis in interpretive semantics.

² The distinction between A, A and B, B is made in connection to the considerations on silence that follow; in reality, A, A and B, B are identical in terms of minimal rhythmic configurations, since they both represent the repetition of a single element.

³ Some works can include foundational socially-normed rhythmic elements like time measured in seconds, hours, etc., and space measured in centimeters, pixels, etc. For example, a painting could reproduce a measuring tape.

⁴ There are three problems with the reproduction of Red-Green Serial Mutation. The reproduction that we are using, whose source remains unknown despite our efforts to find it, begins with the following stripes: light green, dark red, orange, blue, dark green, light red. The reproduction given in Burnett (no date) is a mirror image of our reproduction. Secondly, the opposition light/dark does not stand out well in either reproduction. Lastly, our reproduction cuts off the first and the last stripes.