You are here : Home Page / Theories / Fontanille / The Tensive Model

The Tensive Model

1. Abstract

The tensive model, a device used in post-Greimasian semiotics, was introduced by Fontanille and Zilberberg. In the tensive model, any given value is constituted by combining two "valencies" (or dimensions): intensity and extent (range). Extent is the range over which intensity applies; it corresponds to quantity, variety, and the spatial or temporal range of phenomena. Intensity and extent are each subject to variation on a continuous scale from zero to the maximum (or even infinity). The tensive model is generally represented visually by a graph: intensity is placed on the ordinate and extent on the abscissa. On this graph, any given phenomenon may occupy one or more positions. Two kinds of correlations exist between intensity and extent. The correlation is said to be converse, or direct, if (1) an increase in one of the two valencies is accompanied by an increase in the other and (2) a decrease in one valency causes a decrease in the other. The correlation is inverse if an increase in one of the two valencies is accompanied by a decrease in the other, and vice versa.

This model can be applied to knowledge. If intensity refers to the depth of knowledge and extent to the scope of the field of knowledge, and we distinguish between high and low for both valencies, we obtain four different kinds of "knowers" or knowledge: (1) low intensity and extent (a little knowledge about a few things), (2) high intensity and low extent (a lot of knowledge about a few things), (3) low intensity and high extent (a little knowledge about many things), (4) high intensity and extent (a lot of knowledge about many things). It is generally accepted that the intensity of knowledge can only decrease if its extent is increased, and vice versa (an inverse correlation). A person going into medicine, for example, must choose between a specialty (2) and general practice (3). We should note that the general practitioner's depth of knowledge is described as limited only as compared to the specialist's, not to the average person's, which is disastrously limited.

2. THEORY

2.1 VALUES AND VALENCIES

A device used in post-Greimasian semiotics, the tensive model was introduced by Fontanille and Zilberberg. In the tensive model, any given value is constituted by combining two "valencies" (or dimensions): intensity and extent (range). Extent is the range over which intensity applies; it corresponds to quantity, variety, and the spatial or temporal range of phenomena. Both valencies are quantitative in nature; the first has to do with the measurable, the second with the countable.

NOTE: SOME DETAILS ON VALENCIES

According to Zilberberg (2002, 116), tempo and tonicity are the two sub-dimensions of intensity, while temporality and spatiality are the two sub-dimensions of extent. The functives, or constituent elements, of each dimension are weak/strong for intensity, and concentrated/diffuse for extent (Zilberberg, in press).

In our opinion, temporality and spatiality neglect certain elements that should be covered by extent. In addition to spatial and temporal range, extent has to do with the quantity and variety of phenomena involved, and these things are not always reducible to spatial notions, unless the term is taken metaphorically, in which case it could include concepts, for example (this would apply to the "extent" of knowledge, for instance).

Moreover, when we describe extent as diffuse or concentrated (see Fontanille 2003, 46), thereby implying density, we are implicitly combining two aspects of extent: the quantity of phenomena and their spatial or temporal range. Fontanille (2003, 110) gives intensity and affect, along with an "etc.", as elements that can be plotted on the axis of intensity. So the question arises: Can we put a composite valency on an axis? If so, then we can distinguish between analytic and synthetic approaches to using the tensive model. A synthetic approach allows for the placement of a composite valency on one axis: in this way we can use the axis of intensity to plot the intensity of some element other than the one found on the axis of extent. For example, the intensity of a positive evaluation attributed to knowledge (a compound valency, whereas the intensity of the knowledge itself would be a simple valency) may increase relative to the scope of the knowledge (a simple valency).

2.2 THE STRENGTH OF THE VALENCIES

Intensity and extent are each subject to variation on a continuous scale from zero to the maximum (or even infinity).

As with other devices (the semiotic square, the veridictory square, the actantial model, etc.), the tensive model is simultaneously a network, a conceptual structure and a visual representation of this structure. If we place intensity on the ordinate of a graph and extent on its abscissa, then we obtain a visual representation with two axes.

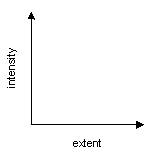
Any given phenomenon will occupy one or more positions on this graph, depending on the degree of intensity it exhibits and the extent over which it ranges. The model may also be represented in table form (we will give an example later).

2.3 VALENCY SECTORS AND ZONES IN THE TENSIVE MODEL

We can delineate different sectors on the tensive scales, and these can vary in number.

2.3.1 DYADIC PARTITIONING

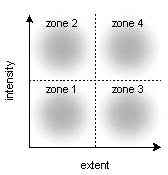
To give an example, if we distinguish two sectors for each valency, a low sector (an inactive sector) and a high sector (or dynamic sector), then we obtain four possible combinations of valencies, which define four zones:

Zone 1: low intensity and low extent
Zone 2: high intensity and low extent
Zone 3: low intensity and high extent
Zone 4: high-intensity and high extent

This would give us the following diagram:

NOTE: PARTITIONING INTO TWO AREAS

Zilberberg (in press) opts for a partitioning into two areas separated by the bisector of the graph. Above the bisector is the area of absolute values, and below it is the area of universal values.

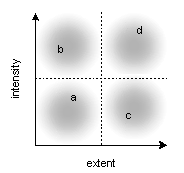
Consider, for example, a group of emotions associated with attachment to other beings. We will distinguish the emotions in this group solely in quantitative terms, although we are aware that a qualitative approach might conclude, for example, that between love and friendship, there is a difference in quality and not (just) quantity. The axis of intensity indicates the intensity of the emotion, and the axis of extent the number of beings toward which a given subject directs this emotion. By partitioning the graph into four zones, we will distinguish four main kinds of emotions. In zone one, we have (a) love (ordinary love); (b) in zone two, "true love", or "the love of a lifetime"; (c) in zone three, we have friendship; and (d) in zone four, "universal love" or compassion. Now we shall refine the analysis. If we distinguish in terms of extent, true love generally applies to fewer beings than ordinary love, and conversely, universal love, as the name indicates, generally applies to more beings than friendship. Then if we distinguish in terms of intensity, friendship is generally a less intense feeling than love, and we consider universal love to be absolute compared to true love, not just in terms of extent but also intensity. This more exact analysis can be represented as follows:

2.3.2 OTHER WAYS OF PARTITIONING

We have given an example of dyadic partitioning, which, when mapped onto two axes simultaneously, generates four zones. However, other methods of partitioning can be used. For example, triadic partitioning might distinguish low, medium and high on one or both axes (see our typology of the 27 curves of aesthetic euphoria (Hébert, in press)); and pentadic partitioning would distinguish five levels, for example: zero, low, medium, high and maximum (or even infinite). Tetradic partitioning on two axes would allow us to attribute a specific zone to each of the four emotions we examined; the other twelve zones created by this partitioning might be appropriate for describing other feelings of attachment.

2.4 DYNAMIC ASPECTS OF THE TENSIVE MODEL

Now we will address the dynamic aspects of the tensive model.

2.4.1 DIRECT AND INVERSE CORRELATIONS

Two types of correlation exist between intensity and extent. The correlation is said to be converse, or direct, if (1) an increase in one of the two valencies is accompanied by an increase in the other and (2) a decrease in one valency causes a decrease in the other. This would be a case of "the more... the more..." or "the less... the less...". The correlation is said to be inverse if an increase in one of the two valencies is accompanied by a decrease in the other, and vice versa. This is a case of "the more... the less..." or "the less... the more...".

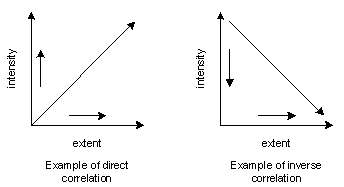
The two kinds of correlations define zones of correlation, which can be approximately represented as follows:

To return to our example of feelings of attachment, the average person is generally subject to an inverse correlation in which the more intense an emotion, the fewer the number of beings to which it applies. For him, universal love is unknown territory.

NOTE: SOME THEORETICAL POSTULATES OF THE TENSIVE MODEL

There is no need to discuss all of the theoretical postulates associated with the tensive model. What we are primarily interested in is its overall functionality, so to speak. However, for the record, here are some of the more important postulates:

1. Intensity and extent make up the content plane (the plane of signifieds) and the expression plane (the plane of signifiers), respectively (Fontanille, 2003, 72). Since any sign originates from the junction of these two planes, any sign is theoretically describable in tensive terms.
2. Intensity is a matter of perception (that is, the perceivable and/or affective feeling, to be discussed later); extent is a matter of understanding (Zilberberg, 2002, 115; Fontanille, 2003, 110).
3. Intensity refers to states of mind (passions); extent to states of things (Zilberberg, 2002, 115).
6. Intensity corresponds to "feelings" (passions); extent to cognition (Fontanille, 2003, 110).
8. Intensity and extent are each broken down into two sub-dimensions: tempo and tonicity for the first; temporality and spatiality for the second (Zilberberg, 2002, 116).
9. The two basic functions of intensity are increase and decrease; the basic functions of extent are sorting (which increases diversity and/or number) and mixing (which decreases diversity and/or number) (Zilberberg, in press).

2.5 ELEMENTARY TENSIVE MODELS

By plotting the converse or inverse tensive correlation as a function of time, we obtain four elementary tensive models:

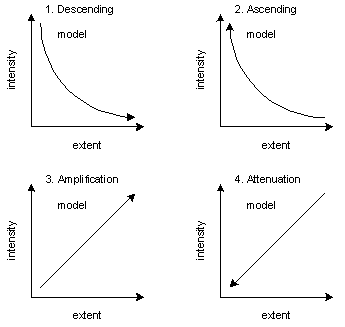
2.5.1 THE DECLINING MODEL

The declining model (or descending model) may be found in the transition between what advertisers call the "hook" (which is strongly affective, but often limited in extent) and the rest of the ad (Fontanille, 2003, 112).

2.5.2 THE ASCENDING MODEL

The ascending model may be found in literature in the transition between the body of a short story and its ending (the climax), which is more limited in extent, but has a higher intensity. The same phenomenon occurs between the body of a sonnet and its ending (or resolution) (Fontanille, 2003, 113).

2.5.3 THE AMPLIFICATION MODEL

The amplification model is found in the majority of symphonic structures, which lead from the barely audible line played by one or just a few instruments into repetitions of growing intensity with more and more instruments (Fontanille, 2003, 113). Ravel's Bolero is an example of this.

2.5.4 THE ATTENUATION MODEL

An example of the attenuation model is a drama with a happy ending or a comedy, where the number and intensity of problems decreases at the end, although they may not disappear entirely.

2.6 COMBINATIONS OF ELEMENTARY TENSIVE MODELS

Two or more tensive models may appear in succession in a semiotic act. When the sequence is a stereotyped one, we use the term "canonical tensive model" (Fontanille, 2003, 110). For example, from the fourth to the fifth act of a classical French tragedy there is an attenuation model (conflicts decrease in number and subside) followed by an amplification model (catastrophe arrives and becomes widespread).

2.7 ORTHOGONAL MODELS

None of the elementary tensive models allows for one valency to remain constant while the other changes; this would result in graphs with horizontal or vertical straight orthogonal lines. But deductively we can predict the existence of phenomena that would need to be described by plotting a line with one constant. (If need be, we could say that the existence of such a phenomenon is attested simply by raising the possibility.) And below we will even see an example of this sort of phenomenon in our analysis of Pascal's theory of knowledge. How many of these orthogonal straight lines might we expect? In dyadic partitioning, we find: two vertical lines, one where extent is at a constant low and the other where it is at a constant high, and two horizontal lines, one of constant low intensity and the other of constant high intensity. Since each of these straight lines may be followed in two different directions (for a constant intensity, extent may be on the increase or the decrease, for instance), this gives us eight new trajectories, for a grand total of 12 kinds.

3. APPLICATION: PASCAL'S THEORY OF KNOWLEDGE

Consider the following thought by Pascal on knowledge (Thoughts, 37, p. 20): "Since we cannot be universal and know all that is to be known of everything, we ought to know a little about everything. For it is far better to know something about everything than to know all about one thing. This universality is the best. If we can have both, still better; but if we must choose, we ought to choose the former. And the world feels this and does so; for the world is often a good judge." The words "all" and "everything" in this reflection are not to be understood literally or absolutely each time, but often in the sense of "a lot". For Pascal, man is caught between the Infinite and Nothing (Thoughts, 72, p. 28), and cannot reach either one.

If intensity applies to the depth of knowledge and extent to the scope of the field of this knowledge, we can establish four different kinds of "knowers" and knowledge.

Pascal makes use of these four zones and ranks them. Since the best zone - the fourth - is inaccessible to men, we must choose the third over the second; the first zone, which is implicit, is held to be of little value; it depicts man's initial state, which he must leave ("we ought to know a little about everything"). A person whose knowledge is at the junction of low intensity and high extent (but above the average person's) corresponds to the classical ideal in which Pascal believed. In contrast to the enlightened man, whose ideal is universal knowledge (for example, the extremely learned Pico della Mirandola), the classical "gentleman" should know, and can only know, a little about everything. The classical conception is based on cognitive pessimism; the humanist conception on cognitive optimism, in which man must somehow compete with a God who knows all about everything.

On another level, two conceptions of knowledge seem to work together in Pascal's philosophy. The first conception, which relates to man's cognitive potential, postulates a constant level of cognitive energy, as it were, and establishes an inverse correlation between the two axes: Just as the pressure of a gas decreases if we increase the volume of space it occupies, so does the intensity of knowledge decrease if we increase the number of objects it encompasses. A converse correlation, in which cognitive energy would vary, is theoretically possible, but is assumed to be impossible in practice. The second conception, which relates to knowledge capital, postulates a possible increase in knowledge by increasing one of the two valencies at a time, either intensity or extent. (A loss of knowledge is not even considered.)

None of the elementary tensive models anticipates a situation where one valency remains constant while the other varies. We could argue that the line going from zone one to zone three is sloped: that the limited intensity of the latter is higher than the limited intensity of the former; in other words, that the apparently horizontal line turns out to be diagonal if we increase the precision of the analysis by allowing for the possibility of multiple positions within one zone. Whatever the case, it is more difficult to make this objection about the line going from zone one to zone two. Increasing the depth of one's knowledge cannot bring about an increase in extent if the increase applies to something already included in the limited initial knowledge. To return to our initial question: How do we integrate a description of these orthogonal straight lines into the tensive model? To present just one of many conceivable solutions let us make a distinction - here and elsewhere, perhaps even in all tensive descriptions - between elementary tensive models, which necessarily imply a converse or inverse relationship, and elementary tensive movements, which cannot exhibit this sort of relationship. Pascal uses only two of these non-converse, non-inverse movements; more specifically, he does not anticipate a transition from zone two to zone one, or from zone three to zone one.

4. LIST OF WORKS CITED

FONTANILLE, J., Sémiotique du discours, Limoges: Presses de l’Université de Limoges, 2003.

HÉBERT, L., "Typologies et segmentations du temps. Les courbes d’euphorie esthétique", in L. Hébert and L. Guillemette (dir.), Signes des temps. Temps et temporalités des signes, Québec: Presses de l’Université Laval (in press).

PASCAL, B., Blaise Pascal: Thoughts, Letters and Minor Works, ed. Charles Eliot, New York: Collier & Son, 1961.

ZILBERBERG, C., Éléments de sémiotique tensive, Québec/Limoges: Presses de l’Université Laval/Presses de l’Université de Limoges (in press).

5. EXERCISE

Add to our analysis of Pascal's philosophy of "knowers" and knowledge by analysing the following thought (Thoughts, 327, p. 113):

"The world is a good judge of things, for it is in natural ignorance, which is man's true state. The sciences have two extremes which meet. The first is the pure natural ignorance in which all men find themselves at birth. The other extreme is that reached by great intellects, who, having run through all that man can know, find they know nothing, and come back again to that same ignorance from which they set out; but this is a learned ignorance which is conscious of itself. Those between the two, who have departed from natural ignorance and not been able to reach the other, have some smattering of this vain knowledge, and pretend to be wise. These trouble the world, and are bad judges of everything. The people and the wise constitute the world; these despise it, and are despised. They judge badly of everything, and the world judges rightly of them."