You are here : Home Page / Theories / Operations of Transformation

Operations of Transformation¹

1. Abstract

Operations, along with relations and terms, are the units that make up a structure. An operation is a process, an action by which an operating subject characterizes or transforms an object (whether the object is a relation, a term, or an operation). Operations of characterization isolate properties of an object by decomposition (mental), classification, typing or categorization, comparison, and other processes. Operations of transformation (1) produce objects (through creation ex nihilo, emanation from a type, or construction from materials known to be pre-existing), (2) destroy them (through annihilation, i.e. with no remaining trace, or through complete deconstruction) or (3) transform them. Continuance is what we have when a given operation (of either characterization or transformation) does not occur. (From a dynamic standpoint, either the operation lacks strength or a counterforce of equal or greater strength is applied.) If one superposes three typologies of transformational operations (Groupe µ's, Zilberberg's and Rastier's), a typology with nine operations is obtained. Firstly, there will be six operations of extensity (on substances): (1) addition (or blending: e.g., A becomes A, B); (2) deletion (or sorting: e.g., A, B becomes A); (3) substitution (e.g., A, B becomes A, C); (4) permutation (e.g., A, B becomes B, A); (5) displacement (e.g., an eye displaced onto the belly of a monster) and (6) continuance (e.g., A, B remains A, B). Secondly, there will be three operations of intensity (on intensities): (7) increase (e.g., from low to high intensity), (8) decrease (e.g., from high to low intensity), and (9) continuance (e.g., an intensity that remains medium).

2. THEORY

2.1 OPERATIONS OF CHARACTERIZATION AND TRANSFORMATION

Operations, along with relations and terms, are the units that make up a structure (see the chapter on structural relations). An operation is a process, an action by which an operating subject characterizes or transforms an object (whether the object is a relation, a term, or an operation). Operations of characterization isolate properties of an object by decomposition (mental), classification, typing or categorization, comparison, and other processes. Operations of transformation (1) produce objects (through creation ex nihilo, emanation from a type, or construction from materials known to be pre-existing), (2) destroy them (through annihilation, i.e. with no remaining trace, or through complete deconstruction) or (3) transform them. Operations of transformation introduce dynamism into a structure. Continuance is what we have when a given operation (either characterizing or transforming) does not occur. (From a dynamic standpoint, either the operation lacks strength or a counterforce of equal or greater strength is applied.) Since the result of continuance is to not change the object (or in partial continuance, to not change it completely), it maintains the ipsative relation between the object and itself, with the object remaining equal (or partially equal) to itself. Henceforth, when we talk about operations of transformation, unless we state otherwise, we will include continuance, even though continuance, in this context, is actually a non-transformation.

2.2 A METATYPOLOGY OF OPERATIONS OF TRANSFORMATION

With a brief discussion of their distinguishing features, three typologies of transformational operations will be merged (which is an operation of transformation): (1) Groupe µ (or Groupe mu, 1982, pp. 45-49; Klinkenberg, 1996, pp. 259-361), whose typology identifies addition, deletion, substitution, and permutation; (2) Zilberberg (2000 and 2005), whose typology distinguishes blending, sorting, increase and decrease, and proposes four degrees of blending/sorting: separation, contiguity, mixing and merging; and (3) Rastier (1987, p. 83), whose typology distinguishes insertion, deletion, insertion-deletion, and continuance. Each of the typologies is supplemented by being superposed with the others, producing a metatypology. In addition, we will fill out the metatypology in various other ways.

Below are the operations we have selected in merging the three typologies; we have excluded some operations, and added one: displacement (although implicit, it is new).

Operations of extensity (on substances)

1. Addition or blending: switch → switcharoo, merde → merdre (Alfred Jarry);
2. Deletion or sorting: petite → p’tite;
3. Substitution (type 1 coordinated deletion-addition): do the dishes → do the gishes;
4. Permutation (type 2 coordinated deletion-addition): infarction → infraction;
5. Simple displacement (simple deletion-addition): an eye displaced onto the belly (see our application below);
6. Extense continuance: merde → merde (in a text by Jarry, instead of "merdre").

Operations of intensity (on intensities)

7. Increase (intensity): rich → super-rich
8. Decrease (intensity): blue → bluish
9. Intense continuance: poor → poor (for someone attempting to become rich).

2.3 DETAILS OF THE METATYPOLOGY

It is not the point of this text on applied semiotics to explain the particulars of the metatypology, the conceptual and terminological choices we have made, or the numerous additions we have planned². It will serve the purpose to give just the most crucial explanations for understanding and applying the theory.

2.3.1 ADDITION/DELETION AND SUBSTITUTION/PERMUTATION

Substitution can be viewed as a coordinated deletion-addition: one element is actually deleted and replaced by adding another. Similarly, permutation can be seen as another form of coordinated deletion-addition: an element located in a position X is deleted, and added in a position Y. Consequently, addition and deletion are the basic operations from which substitution and permutation are derived. This means that simple operations can be combined, either simultaneously or successively, to create a structure.

2.3.2 ADDITION / DELETION AND BLENDING/SORTING

In our view, the opposition addition/deletion is equivalent to the opposition blending/sorting. Of course, the word "addition" evokes an asymmetrical operation, unlike the word "blending" (with addition, X is added to Y, but not Y to X). But our view is that the operations of addition and deletion are a priori neither symmetrical nor asymmetrical. That is, deletion can be symmetrical, as in the breakdown of an atom into its constituents, or asymmetrical, as in the deletion of a letter from a word. The label "sorting" implies a selection, of course, and therefore a classification (or typing or categorization), but sorting should simply be viewed a priori as an un-blending. Whatever the case, addition and deletion presuppose classification, except in random blending and sorting, but even so, these operations also classify, even if ithey do it by no criterion other than chance.

2.3.3 INTENSE SUBSTITUTION, PERMUTATION AND DISPLACEMENT

Intense addition and deletion correspond respectively to increase and decrease. We are not including intense substitution, permutation or displacement, as they can be seen more readily as specific extense operations that apply to intensities as substances (e.g., as semantic features, or semes). For example, if one replaces "very polite" with "not very polite", this can be understood as an extense substitution of the feature (seme) /low intensity/ for the feature /high intensity/. It should be noted that any increase or decrease can be viewed as an operation of substitution, of a higher intensity for a lower intensity or a lower intensity for a higher intensity, respectively.

2.3.4 EXTENSITY/INTENSITY AS A RELATIVE CONCEPT

As in any description, depending on the observing subjects (and on the time of observation, of course), descriptions of intensity and extensity for the same phenomenon can be identical (an interpretive consensus) or different (an interpretive conflict).

The intense or extense nature of any given phenomenon is not absolute, but relative; it can vary according to the universes being described and the observers who found or "inhabit" them – observers whose point of view is being reported. We will use a genocidal person as an example. Compared to a normal human being, does he result from the addition (of cruelty, for example) and/or deletion (of pity, for example) of properties, or from a variation in the intensity (through increase and/or decrease) of properties that any average man possesses (e.g., an increase in cruelty and a correlated decrease in pity)? The answer to this depends on the observer's conception of a human. For Freud, the difference between a normal person and a psychotic person is a matter of varying degrees, not varying natures, and he would no doubt opt for an intense conception of the genocidal person. To take another example, a giant (such as we will see in our application) can be understood as either the result of adding organic matter or of intensifying size. This means that, ultimately, extensities can be "converted" into intensities and vice versa.

2.3.5 DISPLACEMENT AND PLACEMENT

One of the operations that apparently Groupe µ did not directly envisage is simple displacement. A permutation presupposes a coordinated double displacement at minimum (e.g., A, B becomes B, A; where B is now in position 1, and A in position 2). While a displacement of the graphemes (letters, roughly), or phonemes is necessarily a permutation, the same does not necessarily apply in semiotic acts that are not a priori temporal and linear, such as pictorial ones. It is also far from certain that permutation occurs in all displacements of phonemes or graphemes (or more generally, in displacements in the temporal semiotics). For example, if the word "End" is placed at the beginning of a novel rather than at the end, one will sense the underlying displacement, but certainly not the permutation, i.e., the shifting of all the words that follow.

A displacement implies a source space and a target space. Many deletions, additions, and substitutions presuppose displacements (e.g., a marble is deleted from this bag and added into another, or X's heart is replaced with Y's heart, and X's heart is discarded); but others do not (death can be seen as the deletion of life, with no displacement). Both spaces can be situated within tokens (as in our example of a heart transplant) or one of them – the source space – can be within a type. For example, adding an eye to the palm of the hand of a token Tibetan deity (such as Tara) can be considered as an addition with displacement with respect to the humanoid type, in which eyes are located only on the face.

A displacement presupposes a placement, with "placement" simply being another name for "arrangement" (see our chapter on rhythm and arrangement). A placement may be the result of a prior displacement, or not: e.g., the letter that I have put in this word was not located elsewhere previously.

2.3.6 CONTINUANCE

While studying the potential semic transformations between a type signified (the model) and its token (the complete or to some degree deviant manifestation of the model), Rastier predicted the more or less exact counterpart of three operations defined by Groupe µ : addition, deletion³ and substitution. Rastier's typology excludes permutation, which is not relevant, because the semes within a single signified have no position. As for continuance, it occurs when the token signified is completely identical to the type signified (when the meaning of a morpheme in context in a text is exactly the same as the meaning of the morpheme in language). When a token arises from a type, there is the addition of the token, of course; however, if this token is identical to the type, it is a continuance (or perfect reduplication), because it does not constitute a transformation of the type. We will return to this point later.

Rastier's typology differs from the other two in that it is not general. We have considerably generalized the notion of continuance. For Rastier, continuance is in fact the production of a token identical to the type from which it emanates, as we have just seen. In addition, Rastier's transformations are limited to those between a type sememe (the signified of a type morpheme) and a token that belongs to it (this is a type x → token x relation). However, there is no rule against extending them to other kinds of semiotic elements (even though, in our opinion, a continuance always involves a type-token relation as well, as we will see), and to other kinds of relations between types and tokens: type x → type y, type x ← token of x, etc. We will look at a typology of these relations below.

Additionally, we are adding the distinction between marked continuance and unmarked continuance. "Marked continuance" is what we will call the operation by which a unit which, according to the expectations (founded or not) of an observing subject, should have been transformed, but was not. This means that the unit did not match the target type associated with it by the observer. A type is a standardized form defined within a system. We will distinguish the following system levels in particular, for texts, and with adjustments for the other semiotic acts. Going from the higher levels to the lower levels (we are enriching a typology introduced by Rastier, 1989): (1) the dialect (the language system); (2) the sociolect: the usage of a dialect and other standards specific to a particular social practice (rather than a particular social group), which defines the discourses (literary, religious, etc.) and genres (novel, poetry, etc.) of semiotic acts; (3) the idiolect: the particular usage of a dialect, a sociolect and other, strictly idiolectal regularities, which defines the style of a producer. (4) the textolect: the particular usage of the three aforementioned systems and other, strictly textolectal regularities in a particular semiotic act (e.g., a particular text by a particular author); and lastly, (5) the analect: the elements of a semiotic act that do not arise from any system. The minimal (but not necessarily sufficient) condition for a unit to be systematic is to be repeated at least twice.

We will give a simplified example. When Jarry writes "merdre" instead of "merde" in the play Ubu Roi the first time, he creates a discrepancy between the token ("merdre") and the type ("merde"), which we expected it to match. This discrepancy is obviously produced with respect to the dialectal system, since the morpheme "merdre" (or "merdr-", to be more exact) does not exist in the language. When the second "merdre" occurs, the observer can consider that this unit is part of the textolect, i.e., the text's system. He will assume – rightly – that the third token will match the type "merdre" (actually, he could make this assumption for the second token as soon as the first token occurs). When he reads Ubu cocu by the same author and finds a first occurrence of "merdre", he will conclude that this unit is defined as a type in the author's idiolect. Ultimately, each "merdre" of Jarry's is the result of an addition to the dialectal unit, but is a continuance of the textolectal or idiolectal unit. Now if, in some other Ubu sitting in a dusty attic, Jarry had written a thunderous "merde" (instead of "merdre"), this would be a case of deletion with respect to the idiolectal unit, but marked continuance with respect to the dialectal unit. Obviously, the issue of marked continuance would not arise in the case of ordinary French folks writing "merde" in their diaries (especially before Jarry's time), since this unit is expected. Henceforth, unless we indicate otherwise, we will use the word "continuance" by itself to mean "marked continuance".

Continuance takes a variety of specific forms, depending on which transformational operations have not taken place. Thus, continuance might be: non-addition, non-deletion, non-substitution, non-permutation, non-displacement, non-increase, non-decrease (or non- any of the sub-species we will look at, such as non-separation and non-contiguity), and so forth. Clearly, for any one object, a specific form of continuance may have occurred, but not some other.

A problem arises in the typology of operations that has to do with the relations and operations between a type and its token. Strictly speaking, a type is never identical to a token, since they do not have the same status. So technically, a type cannot be said to be conserved [continuance], or reduplicated, or transformed in its token. The same principle applies to operations in the opposite direction, from the token to the type. Whether "identical" or transformed, a token is an emanation from its type. This being the case, we can use methodological reduction (intentional, relevant simplification, explicitly stated) to talk about a type that is conserved, reduplicated (wholly or partially), or transformed in its token, depending on the circumstances.

2.3.7 TYPES AND TOKENS

The main operations of transformation are applied to one or more source elements in order to obtain one or more target elements. Target and source elements can correspond to types (models) or tokens (more or less complete manifestations of the model). Operations can thus act: (1) within a token; (2) within a type; (3) from a type to its token; (4) from the token to its type; (5) from one token to another (of the same type or of a different type); (6) from one type to another. We will give a few examples with patterns, or rhythmic structures. (For more details, see the chapter on rhythmic analysis). The type pattern can simply be kept as is in the token (or from a different point of view, perfectly reduplicated in the token): a particular text might manifest a perfect chiasmus (A, B, B, A). But the type pattern can also be transformed in its token: in A, B, C, B, A, the C can be seen as a delaying element inserted into a chiasmus. The token can be seen as the site of an internal transformation operation: for example, a particular token chiasmus can be seen as the result of a reduplicative addition through reverse permutation (the A, B is followed by the B, A). Clearly, operations can act between a type pattern and another type pattern. For example, groupings (e.g., A, A, B, B) can be seen as the result of a permutation starting from an embedding (the two embedded Bs are simply permuted with the second A in the source pattern A, B, B, A).

2.3.8 GENERATIVE/GENETIC PERSPECTIVES

We will distinguish two perspectives on production: genetic and generative. The generative perspective explains the token as an emanation from a type, or model, which is either complete (when continuance or reduplication is applied) or transformational (when other transformation operations are applied). The genetic perspective conceives the unit as the result of operations on this unit or on parent units.

For example, from a generative perspective, with respect to the type "woman", a siren is produced by substituting the lower body of a fish for the lower body of a woman. From a genetic perspective, we might say the siren is produced through the mating of siren parents, or of one human and one fish parent, or through some very special genetic evolution. Although the meaning of the word "genetic" is also biological in our last example (as in "genetic engineering"), this is not usually the case. For example, a hammer is genetically produced by adding a handle to a head. Although a type is necessarily the starting point for emanations, and thus for generative acts, it can also undergo genetic processing. For example, by producing a male siren and some reverse male and female sirens (i.e., with a fish upper body and a human lower body) the painter Magritte transformed the type "siren", creating new types that emanate tokens.

2.4 SUB-SPECIES OF OPERATIONS

We have already looked at some sub-species of operations for continuance (non-addition, non-deletion, etc.). Obviously, other sub-species are identifiable for other operations, which we do using various criteria. Here we will present some other typologies of sub-species.

2.4.1 SUB-SPECIES PROPOSED BY GROUPE µ

We can distinguish partial deletion (e.g., an apheresis, such as "phone" for "telephone") and complete deletion (e.g., deletion of a whole word).

We can distinguish simple addition (or singulative addition, e.g., epenthesis, such as "merdre" for "merde") and repetitive addition (or iterative addition). We can add to Groupe µ's sub-species by distinguishing between addition by repeating an element already present (e.g., modifying "changes" to "ch-ch-ch-ch-changes" (David Bowie)) and addition by repeating the added element (e.g., modifying "baby" to "little little baby"). A repeated element is necessarily a reduplication (a copy) of another. We propose adding negative (or oppositive) addition. This would be the addition of an element that is the opposite of one already present (e.g., modifying "a good deed" to "a bad good deed" (Balzac)). Contrary to Groupe µ, we take the view that negative operations can occur, not just in substitution, but also in addition and even in permutation. Moreover, we would say that negative operations can apply not just to signifieds, but also to signifiers (for example, in traditional French versification, by adding a feminine rhyme to a masculine rhyme by replacing one with the other, or by permuting them).

We will distinguish between partial substitution (e.g., "do the gishes" for "do the dishes", in which a single grapheme is replaced) and complete substitution (e.g., "body" for "corpse", in which all of the graphemes are replaced). Negative substitution (or oppositive substitution) consists in replacing an element with its opposite (e.g., "What a great idea!" instead of "What a bad idea!" (irony)).

We will distinguish any permutation (e.g., an anagram, such as "lives" for "Elvis" = letters 2, 4, 3, 1, 5 for 1, 2, 3, 4, 5) and permutation by inversion (e.g., "amor" for "Roma" = letters 4, 3, 2, 1 for 1, 2, 3, 4). Negative permutation consists in permuting opposite elements (e.g., changing "big little man" to "little big man").

Addition, deletion, substitution, permutation (more generally, displacement and placement), and continuance can also be characterized according to where the operation is concluded. In this case, the operation is described as initial, medial, or final (occurring at the beginning, in the middle, or at the end of a word, respectively).

2.4.2 SUB-SPECIES PROPOSED BY ZILBERBERG

The distinction addition/deletion can be considered from an incremental perspective or from a categorial perspective (an element is added or deleted, or it is not, with no intermediate position). But this perspective says nothing about the intensity of the blending/sorting operation. In fact, different degrees of blending/sorting must be distinguished. Zilberberg proposes a scale with four intensities; but of course, there is no reason why we could not invent typologies with fewer or more degrees. The diagram below illustrates naïvely, as Zilberberg put it (2000, p. 11), the four degrees of blending/sorting. (The arrows indicate the direction of blending; they must be reversed for the sorting operations).

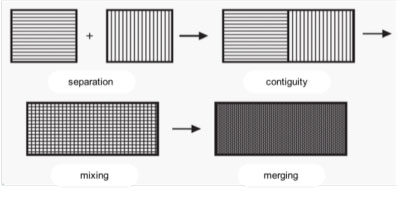
The four degrees of blending/sorting do not act a priori on any specific kind of elements. For example, the elements can be material (e.g., atoms) or immaterial (e.g., semes). So even though a graphic metaphor was used to illustrate the degrees, the elements involved clearly are not necessarily graphic or even spatial.

From a static point of view, four degrees of blending/sorting can be distinguished: separation, contiguity, mixing, and merging. These elements are organized into super-contraries (a strong opposition between tonic or powerful elements) – separation and merging – and sub-contraries (a weak opposition between atonic, or weak, elements) – contiguity and mixing. The opposition super-contraries / sub-contraries was proposed by Zilberberg (2005). It should be distinguished from the opposition contraries / subcontraries found in the semiotic square (see the chapter on the semiotic square).

In absolute merging, the source elements have "disappeared", at least in appearance: (1) through perceptive inability (e.g., no one can see the atoms that constitute an object); (2) through unintentional interpretive reduction (e.g., by someone who does not know that water is made up of oxygen and hydrogen); (3) through intentional interpretive reduction (e.g., pretending as though meringue is not a merging of egg whites and sugar, but an object with no "parts"). There are blends in which the source elements disappear (but their constituents may remain, except in systems that produce complete annihilation): oxygen and fuel disappear in the blend known as fire (undoubtedly a merging).

We will give a simplistic example using a woman and a fish. The simple copresence of a woman and a fish, say, at an outdoor market, is a separation. A chainsaw maniac who juxtaposes a woman's upper body and a fish tail produces a contiguity. A siren would be the mixing of a woman and a fish. A woman with the genetic code of a fish, with no visual clues of her fish nature, would be an example of merging.

A phenomenon's positioning at one stage or another is relatively relative. Consider Magritte's work entitled L’évidence éternelle (1930), which consists of five paintings, each showing different parts of the same woman, hung on the wall from top to bottom so as to reconstitute the woman: the first reproduces her head; the second, her chest; the third, her lower torso; the fourth, her thighs and knees; the fifth, her lower legs and feet. A normal representation of the woman in a single painting would constitute a merging of Magritte's piece, which then acquires the status of a separation. However, if instead of being hung together, the five paintings were distributed among five different rooms of a museum, then Magritte's original work would be a contiguity or a mixing, and the transformed work would be a separation.

From a dynamic standpoint, a blending/sorting operation is a trajectory that goes from an initial stage to a final stage. The typology of elementary trajectories of blending/sorting includes: 1) six elementary trajectories of blending: from separation to merging, from separation to mixing, etc.; 2) six elementary trajectories of sorting: from merging to separation, from mixing to separation, etc.; and (3) four elementary trajectories of continuance: from separation to separation, from merging to merging, etc.

Obviously, trajectories can combine with one another, in succession and/or simultaneity, to form a group, i.e., a structure of elementary trajectories (e.g., from separation to separation + from separation to merging).

A typology of expanded trajectories can be produced if the twelve main elementary trajectories (not including the trajectories of continuance) are used with the two terms of a given opposition placed in the initial stage and final stage (e.g., monster/non-monster or pretty/ugly).This produces 52 expanded trajectories. For example, going from separation to mixing with a man (non-monster) and a horse (non-monster) produces a centaur (monster). Combining expanded trajectories creates a structure of these trajectories. For example, if we combine a trajectory that yields a minotaur (man (non-monster) + bull (non-monster) = minotaur (monster)) and a trajectory that yields a centaur (man (non-monster) + horse (non-monster) = centaur (monster)), we will get a second-generation composite monster, a minotaur-centaur (minotaur (monster) + centaur (monster) = minotaur-centaur (monster)).

The same elements that we have just used to examine blending/sorting operations can be used to look at increases/decreases. From a static perspective, a scale with three degrees could be used: low, medium, and high intensity. From a dynamic perspective, we would then distinguish six elementary trajectories of increase/decrease: from low to medium (increase), etc.; from high to medium (decrease), etc. To these trajectories we can add three trajectories of continuance: from medium to medium, etc. Trajectories can be grouped, either in simultaneity or in succession, in order to define structures. For example, an immediate succession of two trajectories that defines three temporal positions (beginning, middle, end) can take 27 forms: from low to medium + from medium to low, etc. We presented a typology of this sort in the chapter on the tensive model, with intensity being applied to aesthetic euphoria, in that case.

2.4.3 OTHER SUB-SPECIES

2.4.3.1 BALANCED/UNBALANCED OPERATIONS

One aspect that analysis of additions/deletions can incorporate is that of the weighting of the added/deleted elements. In a balanced addition (with no positive connotation), the number of added elements is the same as the number of elements to which the elements are added. The same principle applies to a balanced deletion. The weighting of the elements can have a qualitative impact on the result of the operation. So to give a trivial example, the weighting of oil relative to eggs can make it so that the result will not be mayonnaise.

2.4.3.2 CATEGORIAL/INCREMENTAL OPERATIONS

Like any property (including relations) or any process (including operations), a transformation operation, whether simple or made of a combination of simple operations, can be seen from a categorial or an incremental perspective by any given observer. In the first case, it is considered to be done or not done, with no possibility of partial completion. In the second case, partial completion is possible. For example, while it is possible to add a complete "r" to "merde" and thereby create "merdre", it is not possible to add half of an "r", unless a special graphic game is being played. So the addition and deletion of letters is in fact categorial. Conversely, a chapter of a novel can be partially deleted if some sentences are kept. Any operation that is not fully completed (e.g., an addition) is inversely correlated with a continuance of the same category (e.g., a non-addition): that is, the more transformation there is, the less continuance, and the less transformation, the more continuance.

2.4.3.3 MINIMUM/MAXIMUM OPERATIONS

The minimum transformation operation involves the addition, deletion, displacement, increase, decrease, or continuance of a single unit, or the substitution or permutation of two units. The maximum possible deletion and decrease – when they are total – respectively create the deletion of the relevant unit (e.g., a word is struck out) or its complete attenuation (e.g., a sound whose volume is reduced to zero). Total deletion and decrease are expressions of what we are calling semiotic silence (which is always relative, since there are always elements present). And as for extreme deletion and decrease, they occur just at the boundary before total deletion and decrease; but we should keep in mind that this boundary is always relative as well. If only the head of a character remains in a drawing (there is an example of this in our application), we could call this extreme deletion with respect to the large body parts, but not with respect to the small body parts (like ears, eyes, etc.) : the monster could have been reduced to an eye, or the eye to a pupil, etc.

3. APPLICATION: ICONOGRAPHY OF MYTHICAL BEINGS FROM TIBETAN BUDDHISM

3.1 CORPUS

For our analysis we are using the corpus of mythical beings of Tibetan Buddhism illustrated in black and white in Tcheuky Sèngué's book (2002)⁴. From among the rich depictions of these beings, we will simply look at how the bodies are put together, with some exceptions. And out of the factors of corporeal make-up, we will concentrate on heads, faces, eyes, arms, and legs (or lower bodies).

The corpus contains 270 images in which at least one fantastic being appears. Some beings are represented in many different images (e.g., the Buddha during different periods of his life). Some images include several deities (e.g., the Buddha and his entourage of Bodhisattvas). The same being can take different forms in different images (e.g., a peaceful form and a wrathful or semi-wrathful form, or a peaceful form with two arms and another with four). In addition, we will sometimes mention beings who do not have an iconographic depiction in our reference book, but only a physical description.

In the corpus, the depictions are sociolectally defined within the generic form "iconography of Tibetan Buddhism". We postulate that idiolectal manifestations in this work are relatively rare, since the Tibetan artist, unlike the western artist, does not seek to express a personality, or to improve and/or contest the generic forms. What's more, the drawings in our corpus are clearly not signed, nor even contextualized with a date or place, etc., which makes it problematic to identify idiolectal manifestations, or even more specific generic manifestations (sub-genres).

NOTE: THE TYPOLOGY OF MYTHICAL BEINGS

The mythical beings of Tibetan Buddhism that are represented in the iconography specifically include: (1) the "historical" Buddhas, or Manushi Buddhas, i.e., those who incarnated (as opposed to the "Celestial" Buddhas), among them Shakyamuni (the historically attested founder of Buddhism), the Buddhas who founded the Dharma (Kanakamuni, Kashyapa, etc.) prior to Shakyamuni, and those who come after him (Maitreya, etc.); (2) the other incarnate enlightened beings, some of whom are from legend, and others who are historically attested (Padmasambhava, Milarepa, etc.); (3) the primordial, or Adi Buddhas (Samantabhadra, Vajrasattva, etc.); (4) the five victors, or Dhyani Buddhas (Vairochana, Akshobya, Ratnasambhava, Amitabha, Amoghasiddhi), each of which presides over a "family" of Buddhas; (5) the celestial bodhisattvas, or Dhyani Bodhisattvas (Avalokiteshvara, Manjushri, Tara, etc.); (6) the protectors of the Dharma, some enlightened (Mahakala, Shri Devi, etc.) and some not (Vajrasadhu, Péhar, etc.); (7) some classes of spirits and demons (asparas, asouras, etc.); (8) mythical animals (Kirtimukha) and classes of mythical animals (dragons, garudas, makaras, etc.); (9) the pretas (or hungry ghosts), the asuras (or demigods or Titans), and the narakas (the damned). Devas (worldly gods), asuras, humans, animals, pretas and narakas constitute the six main forms of existence in samsara. Samsara is the conditioned world, and thus the source of suffering, from which one "escapes" through non-abiding (static) nirvana, or which one overcomes through dynamic (unfixed) nirvana, or full enlightenment.

3.2 ADDITION

There is no denying the fact that the corpus favors operations of addition. A goodly number of beings have more than one head and face, more than two eyes, two arms or two legs. The figure of Sitatapattra (2002, p. 258) wins the prize, with 1000 heads, 1000 faces (each of which has three eyes), 1000 arms, and 1000 legs; but 1000-armed Avalokiteshvara is not to be outdone, as we will see.

Faces are added: (1) to a given head (there are no faces without heads); (2) horizontally (there are no faces added vertically to the top of the head); (3) to a principal, central face, and (4) usually, symmetrically on both sides of the central face (e.g., a face on the right, and another on the left, for a total of three faces). Chakrasmavara (2002, p. 204) (and others, like Kalachakra (2002, p. 220)) is a counter example, since he has two faces to the right of his central face and only one to the left.

As for heads, they are added vertically, seemingly the opposite of multi-headed western monsters, whose heads are usually added horizontally. The added heads are always smaller than the head below, e.g., the first head is larger than the second, and the second is larger than the third.

There are seven fantastic beings in the iconographic corpus – all deities – who have multiple, stacked heads. Whereas the volume of the stacked heads can only decrease from one head level to the next, the number of faces will remain stable or decrease from one level to the next, but it will not increase in any case. In other words, the combinatorics here – as elsewhere – is pretty tightly constrained. In the simplest case, apart from the decreases by deincrementing from one level to the next, all of the heads are identical or nearly identical, even if the number of faces varies. Sitatapattra (2002, p. 258) has ten heads with multiple faces, which seem to be topped off with an eleventh identical head that has only one face (however, this would bring the number of faces to 1001, or it simply indicates that the number 1000 is symbolic). Yamantaka's first head (2002, p. 335) is a bull's head, but the three faces on the right are human. The second and third heads are human with only one face, but they appear different. However, these last two heads appear semi-wrathful, and their faces similar or identical to the human faces of the first head, which creates continuity between the three levels.

The numbers of elements of any one kind are clearly symbolic (2002, pp. 38-40). For example, the three eyes, which are seemingly always present on angry (or wrathful) deities, with one exception that we will see later, indicate "simultaneous knowledge of the three times (past, present and future)" (2002, p. 47). The proliferation of body parts on beneficent deities indicates their desire and ability to help all beings.

Operations of addition that affect parts of the body have several other interesting characteristics. Let's look at some of them.

Corporeal additions may consist in adding parts that are absent in the general humanoid type that generates the deity, such as a ring of fire, or wings. Or they may simply add parts that already exist in the type: e.g., two more arms, another eye, etc. Also, the added parts tend to be either identical to the "pre-existing" ones in the original specific type, or almost identical. For example, two more faces identical to the first are added, a second head identical to the first, but smaller, a third eye similar to the other two, but vertical. (But sometimes the eye is not rotated; along with displacement, rotation is one of the possible spatial operations. This is actually a permutation, to be more precise.) However, the faces added to one head are not always identical to the central face; sometimes the difference is minor (Vajrakilaya's different noses (2002, p. 354)) and sometimes the difference is major, such as that between peaceful and angry or humanoid and animal faces (we will come back to this).

Of course, one can distinguish referential adaptations, which alter the actual being who is depicted, and iconic adaptations, which are due to iconographic constraints and conventions. One-thousand-armed Avalokiteshvara's undersized arms may belong to the second category: under-proportioning them makes it possible to show the 1000 arms in an image that is not too large (in actuality, the 1000 arms are not all shown). Under-proportioning the additional heads, on the other hand, seems to be a referential adaptation. That is, even when just one head is added, and not 10 or 11, as in the extreme case of Sitatapattra (2002, p. 258), it is under-proportioned, even though from a pictorial standpoint, two superposed heads of the same size will fit into an image, even if it is small. Whether referential or iconic, we would say that under-proportioning is an intense operation, or more precisely, a decrease.

Moreover, wrathful and semi-wrathful deities always seem to be oversized; we view over-proportioning as resulting from an operation of increase. Increase clearly goes in the same direction as adding arms, heads, etc.: it indicates both the character of the being, and his or her power and desire to help. Over-proportioning is used most notably each time a deity tramples a human body (the corpse symbolizes the death of the ego or the conquest of the negative emotions brought about by the deities). Vajravahari (2002, p. 262) and Kurukulla (2002, p. 254) are obvious cases: Together, the head and the trunk of the trampled corpse are the same size as the deity's foot. The same goes for Vajrayogini (2002, p. 267, see Figure 1). Even so, the proportions in Tibetan iconography are no doubt more expressive than they are "realistic".

Three main types should be distinguished, to which the operations are applied and can be characterized. The first type corresponds to the normal human being; relative to this type, the token – i.e., the fantastic being – may add two wings, two legs, etc. The second type corresponds to a class of deities (e.g., wrathful, semi-wrathful, peaceful; masculine, feminine; etc.). The third type corresponds to the "monster" itself, but minus the operations in question, and elevated to the rank of a type. With respect to this type, in the token there might be, for example, a head added that is identical to the first.

Like any sub-species of operation or any operation, reduplication can be categorial or incremental. From a categorial standpoint, there is reduplication if the added unit (e.g., a left arm) is exactly the same as a unit (the main left arm) found in an encompassing unit (the deity). From an incremental standpoint, a reduplicating unit (e.g., an under-proportioned head) is essentially identical to a reduplicated unit (a head that is not under-proportioned). Reduplication can be simple (e.g., one head or one eye is added) or repetitive (more than one head or more than one eye is added).

We observe that when additions apply to arms or legs, they are made in multiples of two (in our corpus, producing 4, 6, 8, 10, 12, 16, 24, 34 or 1000 arms; 2, 4, 16 or 1000 legs). When faces are added to one head, on the other hand, it is usually done in even numbers, but occasionally in odd numbers (e.g., giving Chakrasamvara four faces for a single head (2002, p. 204)). Heads are added in either odd numbers (which yields four heads on 1000-armed Avalokiteshvara) or even numbers (which yields five heads on 11-faced Avalokiteshvara (2002, p. 182)). The total number of faces is either odd (1, 3, 5, 9, 11 or 1000 faces) or even (4, 8 or 1000).

The added elements have the same characteristics as the elements that they are copying (as in copy and paste) when the elements are eyes (although they may be oriented vertically), arms, or legs. We have mentioned that there can be an adjustment in the form of iconographic (non-referential) under-proportioning.

However, faces are not treated in the same way. They can be added along two axes. On the vertical axis, the faces added above the original face are generally different from it. However, 1000-armed Avalokiteshvara (2002, p. 178, see Figure 2) has three identical heads vertically stacked (but they are decreased by successive deincrementation). However, the fourth head is wrathful, and the fifth head, which is peaceful, depicts the Buddha Amitabha, whose spiritual son is Avalokiteshvara (2002, p. 179). On the horizontal axis, the faces added on both sides of the central face have exactly the same properties as the latter. Some exceptions to this rule can be found: for Yamantaka (2002, p. 335), the faces on the right side (which are human) are not like the central face and the left-side faces (which are bull faces); and one of Rahula's heads (2002, p. 367) has a peaceful main face flanked by two seemingly wrathful faces.

Note that it is less common to have additional legs than additional arms; sometimes the contrast between the addition operation for arms and the continuance operation for legs is striking; this is the case for one thousand-armed Avalokiteshvara, who has two legs.

A third eye always seems to be added to the faces of wrathful deities (except for Ekajati, whom we will soon see), but some peaceful deities are given the same treatment (e.g., Paripurana Tara (2002, p. 252)). The addition of eyes elsewhere on the body seems to be more restricted. One thousand-armed Avalokitheshvara has two eyes for each face, and one eye in the palm of each hand. In addition to the three eyes in her single head, White Tara (2002, p. 242, see Figure 3) has an eye in the palms of her hands and on the soles of her feet. In contrast to faces, arms and legs, which are squeezed in near the elements that they reduplicate, eyes can be added to parts of the body that normally have none (the palms, the soles of feet, the forearms, the nipples, and the belly). Of course, one could say that the eye on Tara's hand is simply added, but relative to the humanoid type, and even relative to the peaceful female Tibetan deity type, there is a displacement from the head to the hand.

Operations of addition for eyes, arms, legs, heads, and faces take place on a core, a recognizable type that is a being of human form, or at least anthropomorphous, as opposed to an animal being, for example. (The outer aspect of many wrathful deities is based on that of the rakshasas, which are beings related to our ogres (2002, p. 439).) Operations of substitution proceed in similar fashion; for example, although the Garuda we will see below is highly composite, nonetheless an original core is still identifiable: a human torso. However, there are strange instances of a being created by pure addition, almost without any basis on which to graft the additions (the additions are then completely symmetrical, a blending of this and that, rather than an addition of this to that), such as the makara, "a sea monster related to the crocodile, but whose composite anatomy is borrowed from a plethora of animals: the lower jaw of a crocodile, the rather long trunk of an elephant, the ears of a wild boar, the eyes of a monkey, the scales of a fish, the mane of a lion, the horns of a deer, etc." (2002, p. 444, see Figure 4). This animal is close to a pure composite; i.e., it is difficult to find a being from which it could have been simply modified (its classification as a crocodile seems rather arbitrary (2002, p. 502)). Moreover, the makara is itself used to produce a monster by substitution. The deity Simhavaktra (2002, p. 334) is created from a human form, but with the head of a makara.

In the ultimate example, the makara is combined with a conch to form a more composite monster yet, elliptically called a "makara" (2002, p. 502). Actually, this makara-conch belongs to a very specific class of animals. In Tibetan Buddhism, three animals symbolize victory over disharmony and disagreement. These mythical animals are forms resulting from a happy resolution of opposites, uniting two animals known to be enemies into one body. They are the otter-fish (known as the "furry fish"), the garuda-lion (known as the "eight-limbed lion"; the garuda is a mythical bird), and the makara-conch (elliptically called the "makara", but which we will call the "makara-conch", and which supposedly feeds on conches) (2002, p. 501). If a Minotaur-centaur is a second-generation composite monster created by combining two beings that are themselves composite, then the garuda-lion and the makara-conch are partly second-generation composite monsters, since just one of the two blended elements in each case is composite itself: the garuda and the makara.

3.3 DELETION

Operations of deletion are underused in the corpus, at least with respect to the aspects that are of interest to us: for example, there is no being with just one eye (with one exception), just one arm, or just one leg (we know that there is a form of one-legged demon, but it is seemingly not pictured or described in our corpus). However, there are two noteworthy exceptions.

In contrast to the figures of reduction that we have seen, there is an astonishing figure of vigorous deletion (the counterpart of vigorous addition), or to be more exact, of extreme deletion. That is, she is right at the boundary before the complete deletion of identical elements (from another standpoint, this would be weak continuance). We are referring to Ekajati. "She is characterized by bodily attributes reduced to oneness: a single braid of hair that stands up, a single eye, which gives her the appearance of a Cyclops, a single tooth resting on her lower lip, and a single breast. Her yellow mustache further reinforces the impression of strangeness that emanates from her." (2002, p. 365). While reducing her to a single eye comes across somewhat like a "mutilation" (which is a genetic operation, occurring directly in the token, since in the depiction there remains a sort of creasing in place of the left and right eyes), the single breast is in the center, which attenuates the effect of deletion that would have resulted from the presence of a single right or left breast. The same principle applies for the centered single tooth.

The mustache has had its natural color (black, brown, etc.) replaced with a color that is supernatural, because it is impossible (yellow). By comparison with Groupe µ's negative substitution (e.g., in irony, where a seme is replaced with the opposite seme), the mustache can be seen as part of a negative addition – i.e., semantically opposed –, since a typically masculine feature is being added to a feminine being. Zilbergerg would call this concessive blending (of elements that are mutually exclusive), as opposed to implicative blending (of indentical or complementary elements): although the deity is feminine, she has a moustache. The internalization of masculine and feminine in the body of a single character is pushed to greater extremes in Maning Nakpo. Also there is nothing in the portrayal of this deity that would reveal it, "Maning Nakpo" signifies "the black eunuch": "By his enuch nature, which is neither male nor female, he transcends the two sexes, thereby symbolizing the ultimate nature" (2002, p. 348, see Figure 5). This nature, which by tradition is considered to transcend oppositions through the neutral term (= neither one) rather than through the complex term (= both) (see the chapter on the semiotic square), is also found in Shri Devi's mount – a mule: "born of the mating of a donkey and a mare, she is neither one. In this sense, she represents the madhyamika, or middle way, which strays neither toward eternalism [the belief in the intrinsic existence of phenomena] nor toward nihilism. What's more, just as a mule is always sterile, the middle way yields no production [karma] in the samsara [our conditioned world]" (2002, pp. 328-329). We would add that since the eunuch is also sterile, he shares the same symbolic interpretation.

The other noteworthy exception using deletion is Kirtimukha, "an animal of which only the head remains (not including the jaw). The Shivaite legend from which he was born informs us that at one time he found himself so deprived of food that he could find no other solution than to consume his own body. Shiva gave him his name, which means "glorious face", and made him the guardian of the threshold of his door⁵. (2002, p. 444, see Figure 6). Note that in the image given of this monster, his hands are seen holding "a golden crest-bar that goes through his mouth" (Beer, 2006, p. 132), so it is not just the head that survived the generalized / maximum deletion (or the weak / minimum continuance). Self-consumption is the result of those operations of transformation in which the operator is the same as the transformed object (as in suicide, self-mutilation, etc.).

3.4 SUBSTITUTION

There are a few substitution operations found in the elements we are studying. The lower body of certain beings has been replaced with the hind part of a snake in the case of Rahula (2002, p. 367) and the nagas (spirits "related to snakes, but also to sirens" (2002, p, 438)), or with a ritual knife (kila) in the case of Guru Drakpur (2002, p. 298). This last substitution is suprising. While it is relatively common to have part of an existing or mythical animal used in substitution, this is the only substitution of an inanimate element for an animate element. Just one other metallic substitution is found in the corpus: one of the pictures of the garuda is entitled "Garuda with metal horns" (2002, p. 435). This is not a case of substituting a metallic object for an organic, animate object (a lower body), but of substituting a metallic material for an organic, and –we would say – inanimate object (the horn).

Other deities, and even some classes of spirits, e.g., the sadaks (2002, p. 440), have had their human heads replaced with animal heads. According to our compilation, these substitutions include the following animals: deer, chamois, horse, goat, dog, owl, crow, cuckoo bird, crocodile, dragon, elephant, hawk, garuda, frog, hoopoe, leopard, lion, wolf, mongoose, bird, bear, brown bear, pig, fox, scorpion, snake, tiger, vulture, and yak. One deity has both humanoid and animal faces: Yamantaka, whose main face and left face are that of a bull (2002, p. 335). Others have one humanoid head, and in their hair, one animal head. For example, Vajravahari has a sow's head in her hair (2002, p. 262). In Maning Nakpo's case (2002, p. 347, see Figure 4), his humanoid hair is what is replaced – with snake tails that go all the way to the ground. This reminds us more than a little of Medusa. One thing seems clear from these two animal additions: that hair is associated with animality.

In theory, a substitution can be localized (e.g., by applying to the head or the lower body), or it can be generalized. The garuda represents this sort of generalized substitution: it is made of a human body whose arms and hands have been kept, but whose head and legs have been replaced with a bird of prey's head and talons, respectively, and to which a bird of prey's tail and wings have been added. This is not exactly a human form with animal influence, but rather an animal form with human influence.

Lastly, a being's seeming can be replaced by some other, while its being remains the same. This substitution is carried out either by changing the temperament status of a single deity (peaceful, semi-wrathful, wrathful), or by changing some other status⁶ (e.g., peaceful two-armed, four-armed, or 1,000-armed Avalokiteshvara; the different aspects of Padmasambhava for a single temperament (2002, pp. 289-298)); or, lastly, by temporarily obscuring their actual seeming. The stories of many deities mention that they temporarily took the form even of particular demonic or evil spirits so as to subjugate them more effectively. This is what Vajrapani, Vajrakilaya, Hayagriva, and others did (2002, p. 196).

4. REFERENCES CITED

BEER, R. (2006), Les symboles du bouddhisme tibétain, Paris: Albin Michel.

GROUPE µ (1982), Rhétorique générale, Paris: Seuil.

HÉBERT, L. (2008), « Petite sémiotique du monstre. Avec notamment des monstres de Hergé, Magritte et Matthieu Ricard", in M.-H. Larochelle (dir.), Monstres et monstrueux littéraires, Québec: Presses de l’Université Laval, pp. 121-139.

KLINKENBERG, J.-M. (1996), Précis de sémiotique générale, Paris: Seuil.

RASTIER, F. (1987), Sémantique interprétative, Paris: Presses universitaires de France.

RASTIER, F. (1989), Sens et textualité, Paris: Hachette.

ST-MARTIN, F. (2010), L’immersion dans l’art, Québec: Presses de l’Université du Québec.

TCHEUKY SÈNGUÉ (2002), Petite encyclopédie des divinités et symboles du bouddhisme tibétain, s.l., Claire Lumière.

ZILBERBERG, C. (2000), "Les contraintes sémiotiques du métissage", Tangence, Rimouski (Québec): 64, automne, pp. 8-24 [republished on the Web: http://www.erudit.org/revue/tce/2000/v/n64/008188ar.pdf].

ZILBERBERG, C. (2005), Éléments de sémiotique tensive, Limoges: Presses de l’Université de Limoges.

5. EXERCISE

Identify the transformation operations for color and shape in Triangulaire (oil on cardboard, 36.5 cm X 21.5 cm, 1972) by the Quebec artist, Guido Molinari (1933-2004). Note that the rotation of a shape is a permutation. For a semiotic analysis of this painting, see Saint-Martin, 2010, pp. 151-179.

¹ This text is an augmented version of Hébert, 2011 (but the conclusion was deleted).

² Further details are found in Hébert, 2008, a text that we are correcting, clarifying, and supplementing here.

³ In a token, the deletion of a seme present in the type creates a state somewhere between presence and absence for this seme, known as virtualization (of an inherent seme, to be more precise).

⁴ Our thanks go to Éditions Claire Lumière (http://www.clairelumiere.com/) for graciously authorizing us to reproduce the illustrations in the book.

⁵ We take the view that "Kirtimukha" is the name of a unique being, and is thus a proper noun, but that "makara" is a common noun that designates a class of beings (thus the lower case letter).

⁶ Another modal series distinguishes the enlightened deities in terms of the particular "body" in which they are represented, of the three bodies they possess: in the nirmanakaya, or emanation body (like Sakyamuni); in the sambhogakaya, or body of glory (like the great majority of the corpus); in the dharmakaya, or absolute body (like Samantabhadra). The resemblance to the Christian deity's three persons is striking, but for lack of space and especially of theological knowledge, we cannot give the points of similarity and difference here.